Dataset Condensation for Recommendation

推荐数据集蒸馏的普遍问题是：

• 对于用户的潜在兴趣，往往会被忽略
• 难以生成离散的user-item交互信息

首先回顾一下推荐数据集蒸馏操作的基本框架

记\(\Phi: U\times I\rightarrow \mathbb{R}\)代表在对应数据集上训练的推荐模型。对于原始数据集\(D\in R^{|U|\times |I|}\)，要找到一个较小的数据集\(D^s\)，其应当满足 \[ \underset{D^s}{argmin}\ \underset{(u,i,r)\sim D^{val}}{\mathbb{E}}[l(\theta_{D^s}^*(u,i),r)]\ \ \ s.t. \theta_{D^s}^* = \underset{\theta}{argmin}\ \underset{(u,i,r)\sim D^{s}}{\mathbb{E}} [l(\Phi(u,i),r)]\tag{1} \] 其中\(D^{val}\)是一个验证集，\(l(\cdot)\)代表对应的可微的loss，其监督模型\(\Phi\)关于用户\(u\)对\(i\)的评分结果。 这是一个经典的数据集蒸馏的双层优化问题，其中内层优化对应的模型，外层优化数据集。这里合成数据集\(D^s\)与\(D\)一样代表user-item交互信息，其应当是参数化的，然后通过\((1)\)式进行优化。

对于第一点，用户未交互的item并不一定是其不感兴趣的，这一隐式关系在原始数据集中通过大量信息的学习也许是可以挖掘出来的，但是当数据集压缩之后，难度可能会变大，因此作者希望在压缩数据集中也能反映出user的潜在感兴趣item。

实现上，首先需要提前训练一个模型\(f_{p}\)，找出每一个user的潜在感兴趣item，这些item应当是user未交互过的，从中取出前topK，作为该user的潜在感兴趣item，形式化来说， \[ TopK(u) = \{ i| i = arg\ \text{IsTopK} f_{p}(u,i'), i'\in I'(u) \}\tag{2} \] 其中\(I'(u)\)就代表\(u\)未交互过的item集合。那么接下来，只需要将 \[ D^{ps} = \{ (u,i)|u\in U, i\in TopK(u)\}\tag{3} \]

加入原始数据集\(D\)，就得到最终增强过的数据集\(D^{p}\)，其保留原始数据集信息的同时，帮助挖掘出了用户的隐藏兴趣，更有利于数据集质量的提升。整体来说，这一操作还是非常自然，符合直觉的，并且从之后的实验来看，这一操作的收益是很大的。 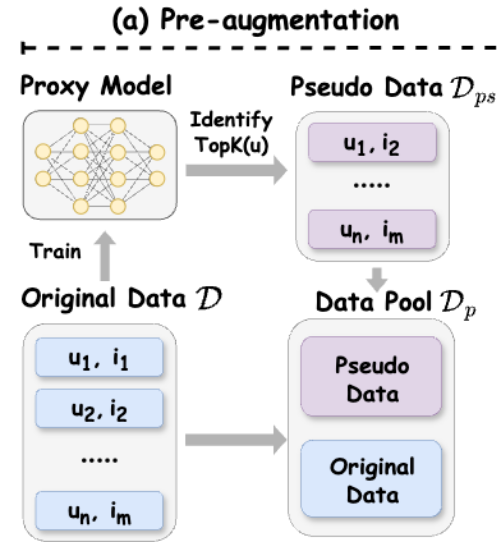关于这里的推荐模型\(f_{p}\)的选择，跟正常做推荐没啥区别，LighGCN，MF，XSimGCL之类的都是可以的，文中也有不同\(f_{p}\)选择的对比实验，这里略过。

接下来是关于离散的user-item交互信息的生成。由于交互信息中，每一个\((u,i)\)对的值只有\(0,1\)两个值，是离散的，并不能直接用梯度下降进行优化。针对这一点，[1]提出重新构造一个参数矩阵\(S\)，\((u,i)\)对的分数\(S_{(u,i)}\in \mathbb{R}\)，然后依据\(S_{(u,i)}\)的大小，采样出较为重要的\((u,i)\)对，用于构造合成数据集\(D^s\)。这里采样操作是不可微的，因此需要调整为gumbal-softmax。此时分数是连续值，因此也就可以用梯度下降来优化了。

关于这一点，本文的思路其实是类似的，同样构造一个参数矩阵\(S\)，但是\((u,i)\)对的分数\(S_{u,i}\in (0,1)\)，然后通过Bernoulli采样得到\(M\)，代表\((u,i)\)是否在\(D^s\)中应该有交互，并用\(M\)构造合成数据集\(D^s\)。即 \[ P(M|S) = \prod_{(u,i)\in D^p}(S_{u,i})^{M_{u,i}}(1-S_{u,i})^{1-M_{u,i}}\tag{4} \] 同时还需要对\(||M||_{0}\)进行限制，因为我们需要限制最终合成数据集的规模，其应当满足 \[ ||M||_{0} \leq r|D|\tag{5} \] 通过\((4)\)式，可以将对\(M\)的限制转化到参数\(S\)上，即\((5)\)式可以转化为 \[ \mathbb{E}_{p(M|S)}||M_{0}|| = \sum_{(u,i)\in D^p}S_{u,i} = ||S||_{1}\tag{6} \] 这就是参数上关于数据集规模的限制，后续\(S\)在进行更新之后，会额外做一步投影操作将其投影到对应的合法空间，即满足\(||S||_{1}\leq r|D|,S_{u,i}\in[0,1]\)的空间内

但是注意到Bernoulli采样操作本身也是不可微的，因此还需要做一些操作。此时外层优化dataset的过程中，Loss表示为 \[ \Phi(S) = \mathbb{E}_{p(M|S)}L(\theta^*(M)), s.t.\ \ \theta^*(M) = \underset{\theta}{argmin}\ \hat{L}(\theta;M)\tag{7} \] 从而梯度可以表示为 \[ \begin{flalign} \nabla_{S}\Phi(S) &= \mathbb{E}_{p(M|S)}L(\theta^*(M))\\ &= \nabla_{S} \int L(\theta^*(M))p(M|S)dM\\ &= \int L(\theta^*(M)) \frac{\nabla_{S}p(M|S)}{p(M|S)}p(M|S)dM\\ &= \int L(\theta^*(M)) \nabla_{S}\ln p(M|S)\ p(M|S)dM\\ &= \mathbb{E}_{p(M|S)}L(\theta^*(M))\nabla_{S}\ln p(M|S)\tag{8} \end{flalign} \] 通过策略梯度，我们现在可以直接估计出Loss对参数S的梯度，并且这一操作只需要forward计算出\(L(\theta^*(M))\)，以及一个非常好算的\(\nabla_{S}\ln p(M|S)\)，这一点只需要对\((4)\)式做一些变形即可。

最终参数\(S\)的更新形式为 \[ S \leftarrow Pc(S - \eta L(\theta^*(M))\nabla_{S}\ln p(M|S))\tag{9} \] 这里\(Pc(\cdot)\)操作就是为了将\(S\)投影到合法空间内

从而，同样是对交互信息进行重参数化建模，同样是有不可微的采样操作以及对应的补救措施，但是本文相对于[1]，实现了一次forward就可以计算梯度，时间上会有巨大的优势，这一点在下图中会更加直观 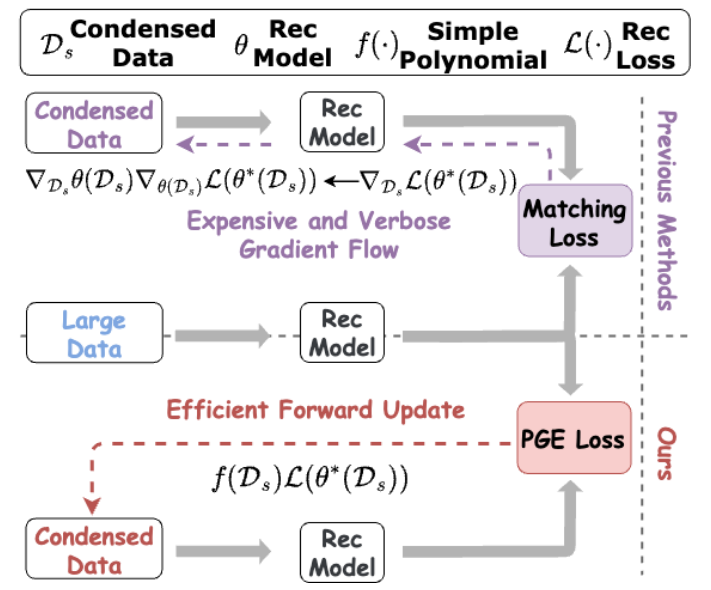此外，为了进一步减少计算成本，内部推荐模型优化的时候，只进行了一步更新，然后就进行梯度对齐。

"The intuition behind is that the loss decreases after first step optimization of the inner model training is strong enough to provide comprehensive information to guide the outer data update"

从下图的结果来看，压缩前先增强数据集这一步的质量收益是很大的，并且one-step update以及REINFORCE极大压缩了计算成本。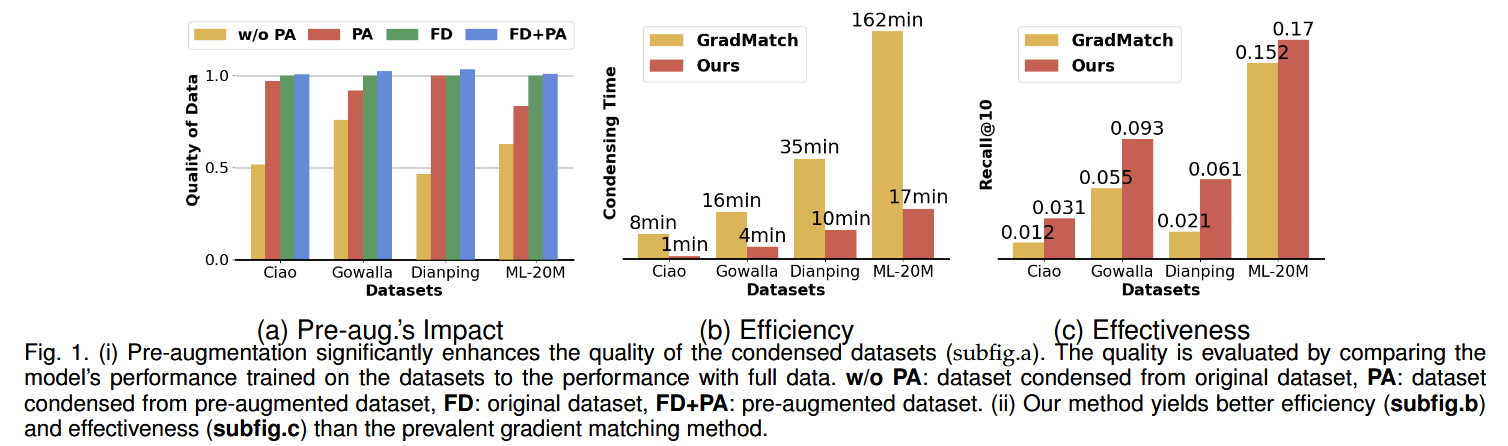

reducing the dataset size by 75% and approximating 98% of the original performance on Dianping and about 90% on other datasets
Besides, our framework is significantly faster than the prevalent gradient matching solver (e.g., 8× in dataset Ciao for updating the data for 100 epochs)

总结一下，压缩前先增强数据集，显式表达user的隐藏兴趣，提升数据集质量。REINFORCE实现前向传播即可估计外层优化的梯度，同时内层优化使用one-step update，压缩计算成本。

Reference

[1] Sachdeva, N., Dhaliwal, M.P., Wu, C., & McAuley, J. (2022). Infinite Recommendation Networks: A Data-Centric Approach. In NeurIPS, 22.