DipSVD: Dual-importance Protected SVD for Efficient LLM Compression

在SVD-LLM的基础上提出改进。LLM matrix decomposition 的目标函数，可以写成 \[ W_{k}^* = \mathop{\text{argmin}}\limits_{W_{k}} ||W_{k}X - WX||_{F}^2\tag{1} \] 每一层的线性层参数\(W\)，以及其输入\(X\)，参数的最优近似结果为\(W_{k}^*\) 引入\(X\)是为了对齐两种参数下的输出结果，但是这对\(X\)的各个通道都是同一权重。作者提出引入 \[ \alpha_{j} = \sqrt{ x_{j}^T(XX^T)x_{j} }\tag{2} \] 这一指标来衡量输入中不同通道的重要性。

实际上这等价于\(||x_{j}^TX||\)，它代表了\(x_{j}\)与各个通道的对齐程度，从而可以反映其重要性。进一步定义重要性矩阵\(D\)，表示为 \[ D_{jj} = \left\{\begin{matrix} a & \text{if } \alpha_{j} \text{ is among the top p\% values},a>1\\ 1 & otherwise \end{matrix}\right.\tag{3} \] 那么目标\((1)\)可以改写为 \[ W_{k}^* = \mathop{\text{argmin}}\limits_{W_{k}} ||W_{k}\tilde{X} - W\tilde{X}||_{F}^2, \ \ \tilde{X} = XD\tag{4} \] 通过系数\(a\)对\(X\)中比较重要的通道进行适当扩大，提高其在之后分解过程中的重要性。

这是从每一层具体矩阵的分解角度出发，另外还可以考虑每一层的压缩率\(k_{i}\)。压缩率会影响每一层SVD分解之后保留的奇异值的数量，但是之前的工作往往是对每一层采用同一个压缩率，或者简单使用二分。这篇文章尝试提出一种自适应的策略。

如果记模型的总层数为\(L\)的话，期望的总压缩率为\(k\)的话，目标可以表述如下 \[ \begin{flalign} &\mathop{max}\limits_{k_{1},k_{2},\dots k_{L}} D(f_{\text{orig}}(x),f_{\text{comp}}(x))\\ &s.t.\ \frac{1}{L}\sum_{i=1}^{L} k_{l} = k \end{flalign}\tag{5} \] 其中\(D(\cdot, \cdot)\)代表衡量两个分布相似程度的手段，作者选择了cos similarity。接下来看看每一层的压缩率\(k_{i}\)可以怎么设置。

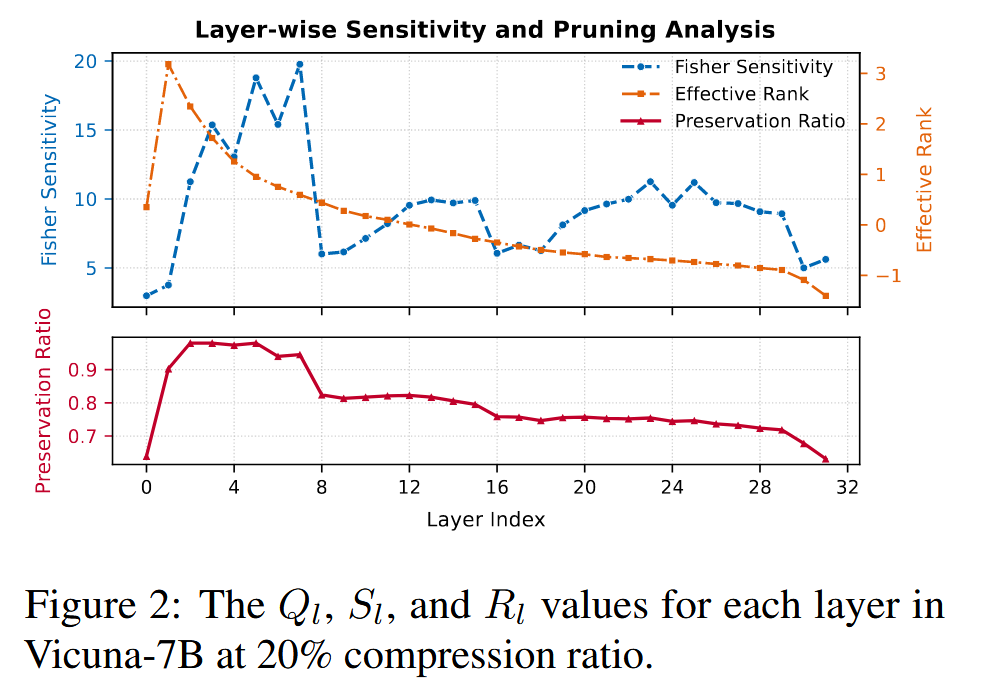
期望衡量每一层的重要程度，以及其可压缩程度。对于前者，作者引入Fisher Sensitivity进行描述 \[ S_{l} = \sum_{Attention} \frac{||\nabla_{\theta}L||_{F}}{||\theta||_{F}} + \sum_{MLP} \frac{||\nabla_{\theta}L||_{F}}{||\theta||_{F}}\tag{6} \] \((6)\)式中，对于每一层的Attention和MLP架构，\(||\nabla_{\theta}L||_{F}\)衡量了该层参数对Loss的贡献，除以\(||\theta||_{F}\)则是为了抹去参数规模的影响，从而得到该层的总体重要程度。\(S_{l}\)越高，该层的重要性越高，从而压缩率应当越高。对于可压缩程度，引入 \[ R_{l} = min\left\{ k| \frac{\sum_{i=1}^{k} \sigma_{i}}{\sum_{i=1}^{r}\sigma_{i}} \geq \text{ threshold} \right\}\tag{7} \]

实际上代表了保留前多少个奇异值得到的信息可以达到预设的阈值threshold，其一般设为\(0.95\) \(R_{l}\)越低，代表这一层可压缩程度越高，压缩率应当越低

那么综合两个指标，可以得到最终指标表示为 \[ Q_{l} = S_{l}^{\beta} (1-R_{l})^{1-\beta}\tag{8} \] 其反映了每一层适合的压缩率大小。那么结合目标\((5)\)，可以得到每一层的具体的参数压缩率为 \[ k_{l} = \frac{Q_{l}}{\sum_{i=1}^{L}Q_{i}}Lk\tag{9} \]

简单来说，就是让一些不那么重要，或者空余参数较多的层，来更多地承担压缩任务。下图展示了Vicuna-7B上不同层的对应系数结果，可以看到前几层往往得到较多保留，而之后的层被压缩的较严重。而之前工作往往对每一层采用同一压缩率，显然是不妥的。