Why Exposure Bias Matters: An Imitation Learning Perspective of Error Accumulation in Language Generation

LM训练的时候，文本前缀用的是ground truth，而推理生成语句的时候，是逐token生成的，文本前缀是自己生成的。由于LM本身生成的前缀相对训练语料分布可能会有很大的偏差，这会导致后续token的生成也出现偏差。这一现象称为 exposure bias。

模型训练的时候，对于不同的前缀\(w_{0}^{t-1}\)，loss可以表示为 \[ l(p_{\theta},w_{0}^{t-1};o) = \mathop{\mathbb{E}}\limits_{w_{t}\sim o(\cdot|w_{0}^{t-1})}\log \frac{o(w_{t}|w_{0}^{t-1})}{p_{\theta}(w_{t}|w_{0}^{t-1})} \] 其中\(w_{0}^{t-1}\)代表到前面生成的长度为\(t-1\)的前缀，\(w_{t}\)代表第\(t\)个生成的token，\(o\)代表目标分布（生成策略） 这实际上就是一个KLD对齐

从而在进行teacher forcing的过程中，总loss表示为 \[ L^{TF}(p_{\theta}) \approx \sum_{t=1}^{T}\ \mathop{\mathbb{E}}\limits_{\substack{w_{0}^{t-1}\sim d_{o}^t \\w_{t}\sim o(\cdot|w_{0}^{t-1})}}\log \frac{o(w_{t}|w_{0}^{t-1})}{p_{\theta}(w_{t}|w_{0}^{t-1})} \]

从而在推理的过程中，可以将模型与目标的偏差表示为 \[ L^{I}(p_{\theta}) = \sum_{t=1}^{T} \mathop{\mathbb{E}}\limits_{\substack{w_{0}^{t-1}\sim d_{p_{\theta},F}^t\\ w_{t}\sim o(\cdot| w_{0}^{t-1})}} \log \frac{o(w_{t}|w_{0}^{t-1})}{p_{\theta}(w_{t}|w_{0}^{t-1})} \] 其中\(w_{0}^{t-1}\sim d_{p_{\theta},F}\)表示前缀由训练的模型得到，\(F\)代表decoding 其记录了\(T\)步累积之后的总偏差

记 \[ \epsilon_{t} = \mathop{\mathbb{E}}\limits_{\substack{w_{0}^{t-1}\sim d_{o}^t\\ w_{t}\sim o(\cdot| w_{0}^{t-1})}} \log \frac{o(w_{t}|w_{0}^{t-1})}{p_{\theta}(w_{t}|w_{0}^{t-1})} \] 代表每一个时间步，模型目标目标分布之后的期望偏差，那么可以得到\(\epsilon=\frac{1}{T} \sum_{t=1}^{T} \epsilon_{t}\)为总体的期望偏差。由此我们不难得到 \[ T\epsilon \leq L^I(p_{\theta}) \leq T^2 \epsilon \] 第一个不等号代表累积误差的期望最小值，即每一步的误差都与上一步无关，误差不会累积，这也是最理想的情况。而第二个不等号代表最坏情况，每一步的误差线性累积，最终表现出二次增长的趋势。

从而可以设计出两个指标： \[ AccErr_{\leq}(l) = \frac{L^I_{\leq l}(p_{\theta})}{\epsilon_{\leq l}} \] 其中\(\epsilon_{ \leq l} = 1/l \sum_{t=1}^{l} \epsilon_{t}\)，代表了前\(l\)步的期望误差 如果exposure bias确实会导致误差累积的话，我们可以观察到\(\text{AccErr}\)值是随着序列长度增加而超线性增长的。 以及 \[ ExAccErr_{\leq}(l) = \frac{L^I_{\leq l}(p_{\theta}) - l \epsilon_{\leq l}}{l \epsilon_{\leq l}} \cdot 100\% \] 其中\(l\epsilon_{\leq l}\)是这\(l\)步的最小损失，所以\(ExAccErr\)值代表多出来的损失所占的比重，而这实际上就是由损失累积带来的。如果一个模型能够做到每一个的损失不会累积的话，那么这个值应当一直在0左右，否则，就会呈不断上升的趋势。

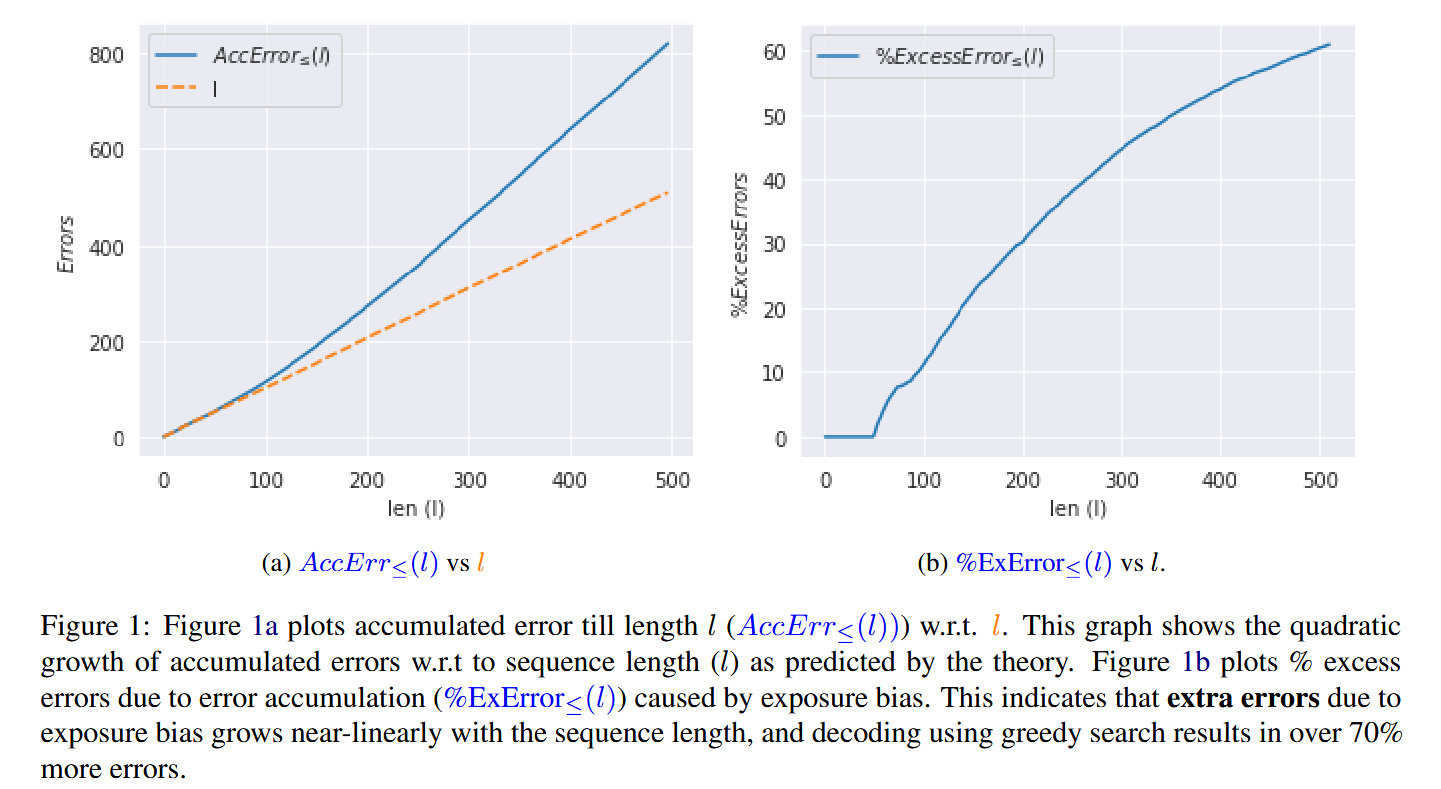
下图\((a)\)给出了AccErr值的变化曲线，以及l的线性增长曲线，可以看到AccErr确实是超线性增长的，这肯定了损失累积现象。并且可以看到AccErr的增长是接近二次的，而这一点在\((b)\)中可以观察到，每一步的多余累积误差是线性的，两者可以相互印证。这也证明损失累积的程度是比较大的。

另外一个有意思的点是，目前模型推理生成token时，所使用的指标往往是困惑度，而 \[ \begin{flalign} \epsilon &= \frac{1}{T} \sum_{t=1}^{T} \mathop{\mathbb{E}}\limits_{\substack{w_{0}^{t-1}\sim d_{o}^t\\ w_{t}\sim o(\cdot| w_{0}^{t-1})}} \log \frac{o(w_{t}|w_{0}^{t-1})}{p_{\theta}(w_{t}|w_{0}^{t-1})}\\ & \approx -\frac{1}{|D|} \sum_{\substack{(w_{0}^{i-1}, w_{i})\in D}} \log p_{\theta}(w_{i}|w_{0}^{i-1}) + c\\ &=H(p_{\theta}; D) + c' \end{flalign} \] 这里\(H(p_{\theta}; D)\)代表log 困惑度

从而我们不难发现困惑度所关注的内容与\(\epsilon\)是类似的，只能捕捉单步的损失，但是对多步累积的损失无法监督，这也是可以尝试突破的一个点。