Proximal Gradient and Subgradients
Proximal Gradient
在对函数做梯度下降的时候，一般要求其是可微的，但这种情况并非总是成立。面对 \[ min_{x}f(x)+g(x)\tag{1} \] 其中\(f\)可微，但是\(g\)不是，那么普通的梯度下降就不能使用了，此时可以采用Proximal Gradient： \[ x_{k+1} = \text{prox}_{\lambda_kg}(x_k-\lambda_k \nabla f(x_k))\tag{2} \] 这要求：
- \(f\)是
L-Lipschitz光滑的 - \(g\)是凸函数（但是并不要求光滑）
按照\((2)\)式迭代更新\(x\)即可。\((2)\)式可以看成两个部分：右边就是一个正常的对\(f\)的梯度下降，外面\(\text{prox}\)是近端算子
近端算子
其定义为 \[ \begin{flalign} \text{prox}_{\lambda g}(w) &= argmin_{z} \frac{1}{2\lambda}||w-z||^2_{2} + g(z)\\ &=argmin_{z} \frac{1}{2} ||w-z||_{2}^2+\lambda g(z)\tag{3} \end{flalign} \] 其中\(\lambda\)是学习率。这个式子实际上是在求点\(w\)附近一个可以使得\(g(z)\)足够小的\(z\)。代入\((2)\)式我们可以发现，这里\(w\)实际上对应了\(f\)梯度下降后的next-state，从而这种操作本身是在两个函数优化之间做了trade-off
接下来可以看一下从这种定义出发是如何近似\((1)\)式的 \[ \begin{flalign} x_{k+1} &= \text{prox}_{\lambda_kg}(x^k-\lambda_k \nabla f(x_k))\\ &= argmin_{z} \ g(z) + \frac{1}{2\lambda_k} ||x_k-\lambda_k \nabla f(x^k) - z||^2_{2}\\ &= argmin_{z} \ g(z) + \frac{\lambda_k}{2} ||\nabla f(x_k)||_{2}^2 + \nabla f(x_k)^T (x_k-z) + \frac{1}{2\lambda_k}||x_k-z||_{2}^2\\ &= argmin_{z}\ g(z) + f(x_k) + \nabla f(x_k)^T (x_k-z) + \frac{1}{2\lambda_k}||x_k-z||_{2}^2\\ &\approx argmin g(z)+f(z) \end{flalign}\tag{4} \]
倒数第二个等号，用\(f(x_{k})\)替换\(\frac{\lambda_k}{2} ||\nabla f(x_k)||_{2}^2\)是因为它们都跟\(z\)没有关系，最后一个等号，\(f(x_k) + \nabla f(x_k)^T (x_k-z)\)用来线性近似\(f(z)\)，后面一项用来控制近端误差，保证\(z\)与\(x_{k}\)不会太远，从而线性近似足够有效。整体来说，可以保证\(x_{k+1}\)是\(x_{k}\)附近使得\(g(\cdot)+f(\cdot)\)足够小的一个点。
此时我们还有一个非常重要的问题：\((3)\)式要怎么求？实际上对于一般的凸函数\(g\)，想要直接求解\((3)\)式也不容易，因此这种方法一般也只对某些好求\((3)\)式极值点的\(g\)有效。
两个例子
常用的有\(g(x)=||x||_{1}\)，此时有 \[ \text{prox}_{\lambda g}(x) = argmin_{z} \frac{1}{2\lambda}||x-z||_{2}^2 + ||z||_{1}\tag{5} \] 其每一个分量的最优解为 \[ z_{i}^* = \begin{cases} sgn(x_{i})(|x_{i}|-\lambda) & \text{if } |x_{i}|>\lambda, \\ 0 & \text{if } else. \end{cases}\tag{6} \]
而当 \[ g(x) = I_{C}(x) = \begin{cases} 0 & \text{if } x\in C\\ \\ \infty & \text{if } x\notin C \end{cases}\tag{7} \] 时，近端算子就退化到了集合\(C\)上的投影，因为如果\(x\notin C\)的话，根本就找不到最小值，从而 \[ \text{prox}_{\lambda g}(x) = argmin_{z} \frac{1}{2\lambda}||x-z||_{2}^2 + I_{c}(x) = argmin_{z\in C}||x-z||_{2}^2\tag{8} \]
Subgradients
尝试解决的问题与Proximal
Gradient类似，都是处理不可微场景的。具体来说，对于一个不可微的点，其无法计算梯度，从而不能正常优化。为此引入次梯度，定义为
\[
\partial f(x) = \{ g| f(y)\geq f(x) + g^T(y-x) , \forall y\in
\text{dom}f\}\tag{9}
\]
直观理解的话，就是下图中点x处的任意支撑超平面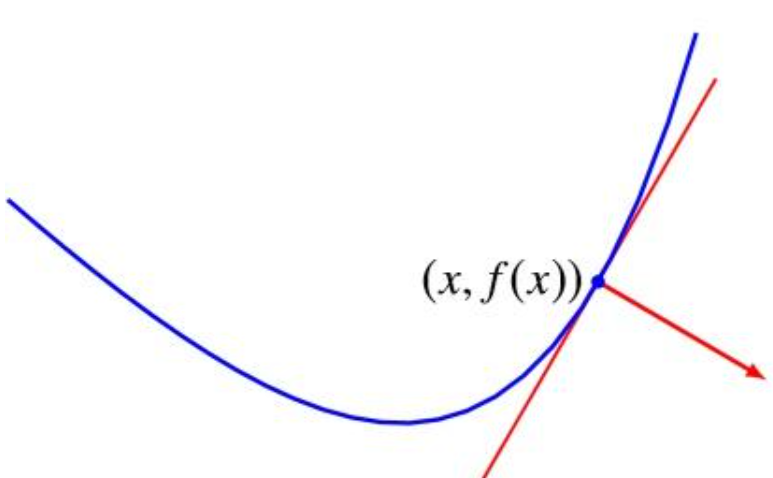
当\(f(x)=x\)的时候，有 \[
\partial f(x) = \begin{cases}
sign(x) & \text{if } x \neq 0\\ \\
[-1,1] & \text{if } x =0
\end{cases}\tag{10}
\]
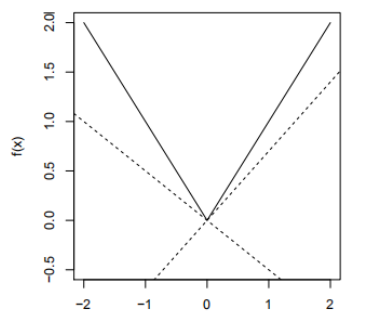这一点并不难理解。
性质
次梯度作为一个集合，存在如下性质
- \(\partial f(x)\)是一个闭凸集，哪怕\(f\)是非凸的，这一点也是成立的
- 当\(f\)在点\(x\)可微的时候，\(\partial f(x) = \{ \nabla f(x)\}\)
- 当\(\partial f(x) = \{ g\}\)时，\(f\)在点\(x\)可微且\(\nabla f(x)=g\)
例子
对于任意\(f\)， \[ f(x^*)=min_{x} f(x) \iff 0\in \partial f(x^*)\tag{11} \] 这是非常有意思的一点。以往用梯度的时候，点\(x\)是极小值点能说明\(\nabla f(x)=0\)，但是反过来并不成立，而用次梯度来思考的话，这成了一个等价条件。这里我们只需要证明必要性： \[ \forall y\in \text{dom} f,f(y) \geq f(x^*)+0^T(y-x^*)=f(x^*)\tag{12} \]
利用次梯度还能证明一阶必要条件：
首先极值问题等价于： \[ min_{x} f(x)+I_{C}(x)\tag{13} \] 当点\(x^*\in \Omega\)是函数\(f\)的局部极值点时，有\(0\in \partial(f(x)+I_{C}(x))\)，从而 \[ \begin{flalign} & \iff 0\in \{ \nabla f(x) \} + N_{C}(x)\\ & \iff -\nabla f(x)\in N_{C}(x)\\ &\iff -\nabla f(x)^Tx\geq -\nabla f(x)^Ty , \forall y\in C\\ &\iff \nabla f(x)^T(y-x)\geq 0, \forall y\in C \end{flalign}\tag{14} \] 其中\(N_{C}(x)\)是\(I_{C}(x)\)的次梯度 \[ N_{C}(x) = \{ g\in R^n| g^Tx \geq g^Ty, \forall y\in C \}\tag{15} \]
在Proximal Gradient中我们看过一个近端算子的形式为 \[ \text{prox}_{\lambda g}(x) = argmin_{z} \frac{1}{2\lambda}||x-z||_{2}^2 + ||z||_{1}\tag{16} \] 它有一个更加normal的形式，被称为LASSO \[ argmin_{\beta\in \mathbb{R}^p} \frac{1}{2}||y-X\beta||_{2}^2+\lambda||\beta||_{1}\tag{17} \] 这里\(y\in \mathbb{R}^{n}, X\in \mathbb{R}^{n \times p}\)。我们同样可以用次梯度来分析这个问题 \[ \begin{flalign} & 0\in \partial(\frac{1}{2}||y-X\beta||_{2}^2+\lambda||\beta||_{1})\\ & \iff 0\in -X^T(y-X\beta) + \lambda \partial||\beta||_{1}\\ & \iff -X^T(y-X\beta)\in \lambda \partial||\beta||_{1}\\ & \iff \exists v\in \partial||\beta||_{1}, s.t.\ X^T(y-X\beta)=\lambda v \end{flalign}\tag{18} \] 我们仔细分析一下\(g=\partial||\beta||_{1}\)，注意到\(||\beta||_{1}=\sum_{i} |\beta_{i}|\)，各分量相互独立，从而 \[ g_{i} = \begin{cases} \{ sign(\beta_{i}) \} & \text{if } \beta_{i}>0 \\ [-1,1] & \text{if } \beta_{i}=0 \end{cases}\tag{19} \] 从而这为我们给出了最优解\(\beta\)关于\(y\)必须满足的两个关系： \[ \begin{cases} X^T(y-X\beta)=\lambda sign(\beta_{i}) & \text{if } \beta_{i} \neq 0 \\ |X^T(y-X\beta)|\leq \lambda & \text{if } \beta_{i}=0 \end{cases}\tag{20} \] 这实际上是一种soft-thresholding行为，从而利于导出稀疏的\(\beta\)解，而这也正是\(L_{1}\)正则化最重要的作用。