BOND: Aligning LLMs with Best-of-N distillation
Main
Best-of-N是一个很好的推理时策略，但是需要进行N次推理，成本有点大，作者希望进行一次推理就能达到与其一致的生成效果。作者的想法是，抽象出BoN的策略\(\pi_{BoN}\)，然后让模型策略\(\pi\)与\(\pi_{BoN}\)进行对齐。这其实也可以看成是一种蒸馏。
\(\pi_{BoN}\)显式建模出来的结果是 \[ \pi_{BoN}(y) = \pi_{ref}(y) \times p_{\leq}(y)^{N-1} \times \sum_{i=1}^{N} \left[ \frac{p_{<}(y)}{p_{\leq}(y)} \right]^{i-1}\tag{1} \] 具体证明参考论文Appendix A.。其中\(\pi_{ref}\)是原始策略，\(p_{\leq}(y) = \mathbb{P}_{y' \sim \pi_{ref}}[r(y')\leq r(y)]\)代表依据\(\pi_{ref}\)生成的token \(y'\)，依照奖励模型\(r\)，不优于\(y\)的概率，\(p_{<}(y)\)也是同理。
作者还提供了BoN与RLHF的关系。RLHF的目标一般是 \[ \pi_{RLHF} = argmax_{\pi} \mathbb{E}_{\pi}[r(y)] - \beta D(\pi||\pi_{ref})\tag{2} \] 一方面希望尽可能获得更多的奖励，同时要求学习到的策略与原始策略不要偏离太远。根据上式可以得到\(\pi_{RLHF}\)的显式解，简单表示为 \[ \pi_{RLHF}(y) \propto \pi_{ref}(y)\exp\left( \frac{1}{\beta}r(y) \right)\tag{3} \] 证明可以参考[1] (Appendix A)。将\((1)\)与\((3)\)的形式进行对比，实际上就可以得到\(\pi_{BoN}\)下的奖励函数 \[ r_{BoN}(y) = \log p_{\leq}(y) + \frac{1}{N-1} \log \sum_{i=1}^{N} \left[ \frac{p_{<}(y)}{p_{\leq}(y)}\right]^{i-1}\tag{4} \] 这里\(\frac{1}{N-1}\)是\(p_{\leq}(y)^{N-1}\)带来的。同时不难注意到此时RLHF中关于KL项的系数\(\beta = N-1\)，这为理解BoN提供了RLHF的视角。即BoN中的采样次数\(N\)，代表了RLHF中KL项的约束强度。N越大，\(\beta\)越大，越倾向于在RLHF中进行KL对齐。
同时，\(r_{BoN}\)中每一项都是log的形式，因此其对于较高值并不会有明显偏大的奖励，但对较小值会有很大的惩罚，相比起鼓励good case，BoN其实更加侧重于避免bad case。此外，不管是\(p_{\leq}(y)\)还是\(p_{<}(y)\)，提供的都是相对大小，或者说rank信息，因此其对reward会更加鲁棒。这段分析还是很有意思的。
不管怎么样，根据\((1)\)式，接下来可以以\(\pi_{BoN}\)作为学习目标，尝试得到BoN的生成效果。这里涉及三个问题
如何计算\(p_{<}, p_{\leq}\)
如何对齐两个策略，即\((2)\)式中\(D\)的选择
N的选择
对于第一点，作者选择直接蒙特卡洛采样进行估计，表示为 \[ \hat{p}_{\leq}(y) = \frac{1}{k}\sum_{i=1}^{k} [r(y_{i})\leq r(y)]\tag{5} \] 对于第二点，KL和RKL各有优劣，作者选择将两者进行加权结合，也称为Jeffreys divergence。这一选择与之前的认知[2]相符
最后，关于\(N\)的选择，其影响如下
一个大的N，可以带来好的效果，但是可能带来更大误差，以及成本大。作者选择用一种迭代的方式来近似一个大的N的效果。
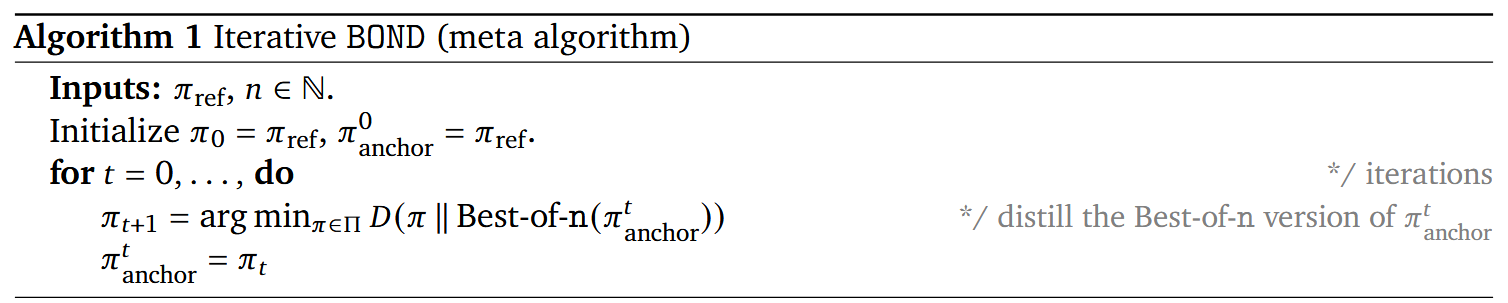基于的事实是，在一次BoN优化之后，再进行一次BoN优化，相当于做了一个Bo\(N^2\)的优化。因此最后实现时，每次只需要取\(N=2\)，然后多次迭代来更新策略\(\pi\)
非常优雅的一篇文章。
Reference
[1] Rafailov, R., Sharma, A., Mitchell, E., Ermon, S., Manning, C.D., & Finn, C. (2023). Direct Preference Optimization: Your Language Model is Secretly a Reward Model.