Delta Knowledge Distillation for Large Language Models

LLM蒸馏中，指出学生直接模仿教师的分布是欠妥的，因为两者的能力不同，可以尝试学习教师从预训练到SFT后的转变路径。

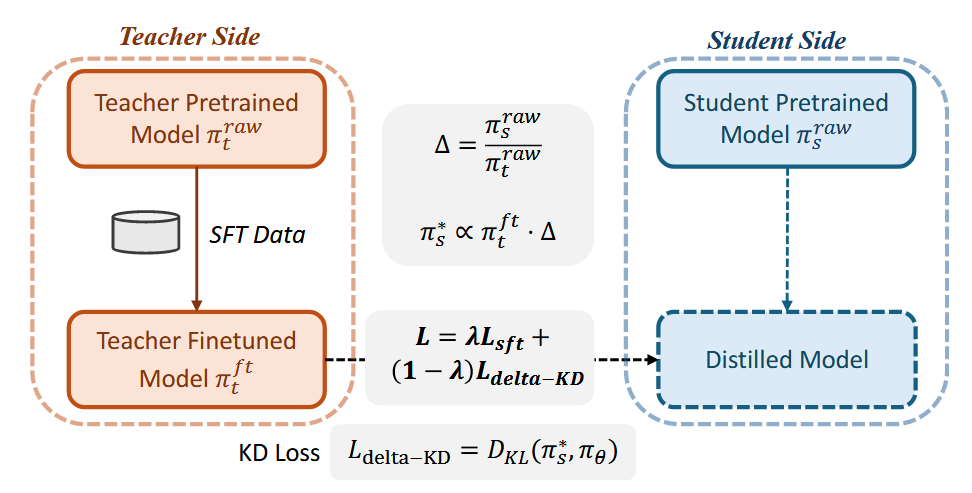
具体来说，给定\(\pi_{s}^{raw}(y|x)\)代表学生的原始预测分布，\(\pi_{t}^{raw}(y|x)\)代表教师SFT前的预测分布，\(\pi_{t}^{ft}(y|x)\)代表教师SFT之后的预测分布，希望找到一个目标分布\(\pi_{s}^*(y|x)\)，能够借鉴到教师从预训练到SFT之后的转变 > align the finetuning trajectory of the small model with that of the large model by matching their respective behavior shifts

记 \[ \Delta(p_{1},p_{2})(y|x) = \frac{p_{1}(y|x)}{p_{2}(y|x)}\tag{1} \] 代表目标分布\(p_{1}\)，原始分布\(p_{2}\)之间的相对关系，那么对于上述内容，可以表述为 \[ \Delta(\pi_{s}^{*}, \pi_{t}^{ft})(y|x) \propto \Delta(\pi_{s}^{raw}, \pi_{t}^{raw})(y|x)^\alpha \tag{2} \] 这里\(\alpha\)用于控制对齐的强度。将\((1)\)代入\((2)\)之后，可以得到 \[ \pi_{s}^*(y|x) = \frac{1}{Z(x,y)} \pi_{t}^{ft}(y|x) \left( \frac{\pi_{s}^{raw}(y|x)}{\pi_{t}^{raw}(y|x)} \right)^\alpha \tag{3} \] 其中\(Z(x,y)\)是归一化项

然后用KLD将学生参数分布\(\pi_{\theta}(y|x)\)与目标分布\(\pi_{s}^{*}(y|x)\)进行对齐即可。同时添加与ground truth的对齐。 这种完全增量的更新目标相对以前还是挺不一样的，有一定道理，值得借鉴。