LANGUAGE MODEL COMPRESSION WITH WEIGHTED LOW-RANK FACTORIZATION

指出模型matrix decomposition的时候，依据singular values的大小贪心删去对应方向的向量，与模型性能减少的幅度，可能并不是完全正相关的

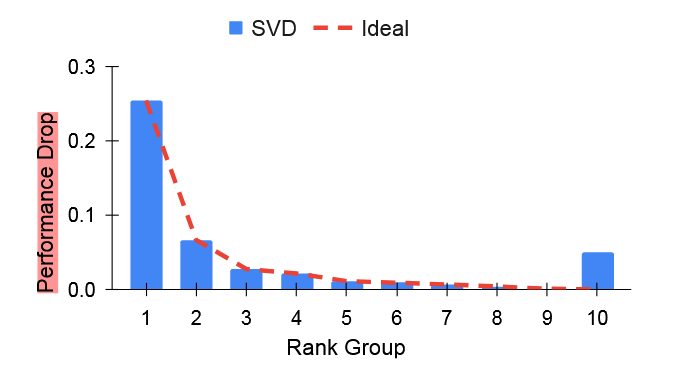
可以看到，这里删去最小的一组singular values反而导致了比前几组更多的性能下降。这是因为单纯对参数进行SVD分解，并没有考虑到data，task

我们记模型的SVD分解结果为 \[ W = U\Sigma V \] 可以简记为\(A = U\Sigma,B=V\) 那么原本的目标可以表示为 \[ \mathop{min}\limits_{A,B}||W-AB||_{2} = \mathop{min}\limits_{A,B}\sum_{i,j}(W_{i,j}-(AB)_{i,j})^2\tag{1} \] 本文考虑对每一个参数进行加权，依据为参数与性能的关联性，从而新的目标可以表示为 \[ \mathop{min}\limits_{A,B}\sum_{i,j}\hat{I}_{W_{i,j}}(W_{i,j}-(AB)_{i,j})^2\tag{2} \] 接下来的问题就是如何能够得到参数与性能之间的关联？可以使用Fisher information，其定义如下 \[ I_{w} = E\left[ \left( \frac{\partial}{\partial_{w}}\log p(D|w) \right)^2 \right]\approx \frac{1}{|D|}\sum_{i=1}^{D} \left( \frac{\partial}{\partial_{w}}L(d_{i};w) \right)^2 = \hat{I}_{w}\tag{3} \] 其中\(d_{i}\)代表具体训练数据，\(L\)就是任务相关的loss。直观来看，这一指标实际反映的就是在参数\(w\)下，模型期望loss。那么对于那些改变之后对\(\hat{I}_{w}\)影响较大的参数，就应当是需要重点拟合的参数，相对应的，在\((2)\)式中，也应该给到更大的权重。

当然，\((2)\)式此时还缺乏一个闭式解，因此需要对齐做一个近似：每一行的参数取同一个权重： \[ \hat{I}_{w_{i}} = \sum_{j} \hat{I}w_{i,j}\tag{4} \] 从而\((2)\)式可以整理为 \[ \mathop{min}\limits_{A,B}||\hat{I}W-\hat{I}AB||_{2}\tag{5} \] 从而我们只需要对\(\hat{I}W\)进行SVD分解，分解出来的结果作为\(\hat{I}AB\)即可。

最后展示一下目前已有的模型压缩技术路线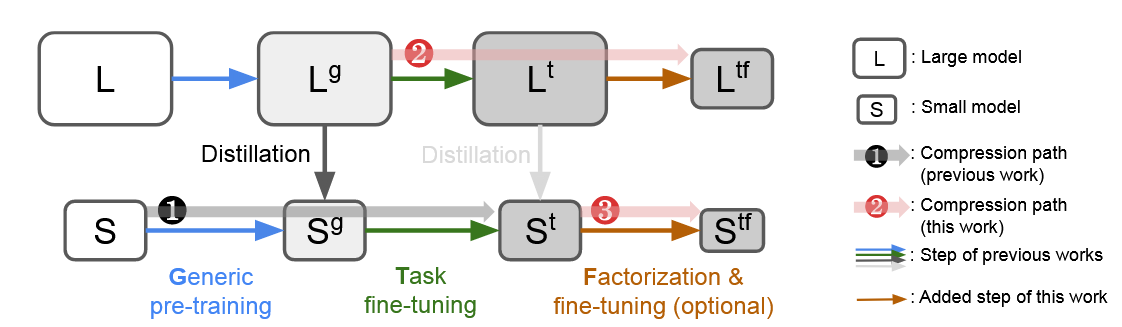

对于LLM，一般是先做预训练，然后针对特定任务微调，最后post-training进行参数压缩，post-training中已有的技术包括Quantization，参数剪枝，以及本文的Factorization。如果有学生模型的加入的话，在双方都预训练之后，可以做一个KD，然后做类似的微调。早先的操作中，学生在KD，微调之后基本就结束了，但是本文的引入可以做到在后面再加一个Factorization，对学生再进一步压缩参数。作者的实验表明这一操作确实是有效的。

事实上，对于KD，其实学生模型的架构是提前限定好的，但是model每一层具体可以怎么压缩，压缩到什么程度，直接提前设定好是否还是欠妥，事实上应该也很难提前确定好最优解。而进一步向最优解靠近交给Matrix Decomposition来自适应调整，或许是比较好的。这样一来，KD用于知识迁移，MD用于冗余参数移除，两者的功能其实还是相对正交的。因此路线3的合理性也是可以理解的。