关于浮点数存储精度

关于浮点数存储精度：IEEE-754浮点标准

背景

炼丹时常用的数据类型有FP32，FP16，其数据存储类型都遵循IEEE-754浮点标准，展示如下

单精度（FP32） 符号位：1位 指数位：8位 尾数位：23位 总范围：\(\pm 3.4\times 10^{38}\)

半精度（FP16） 符号位：1位 指数位：5位 尾数位：10位 总范围：\(\pm 65504\)

关于这些不同的位具体是如何组成浮点数的，详细内容可以参考这篇文章，接下来以FP32为例简单解释一下

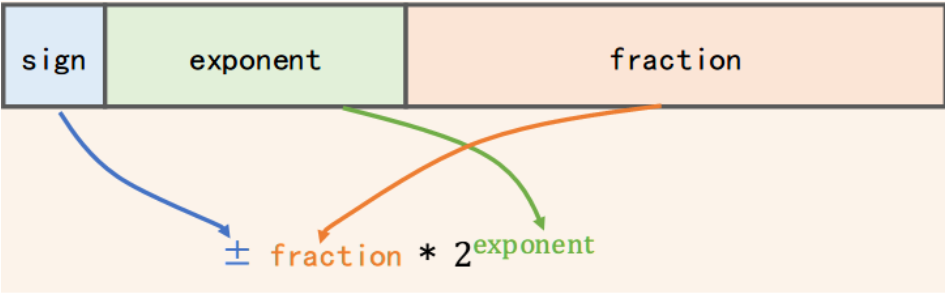
• 符号位 符号位（sign）很好理解，0/1分别用于表示数字的正/负

• 尾数位 尾数位记录的是浮点数的二进制表示，并且将小数点移到第一位之后，然后去除第一位，因为其一定是1（这里先不考虑0） 比如考虑小数10.75 其二进制表示为 1010.11 这是因为10.75=2+8+1/2+1/4，然后将其小数点左移，得到\(1.01011\times 2^3\),那么尾数就是01011，剩下的位直接用0来补即可 FP32下不难得到尾数位的表示范围为\(2^{23}\)

• 指数位 指数位顾名思义，组成的是尾数位的指数，FP32下规定其表示范围为\([-127,128]\)，也就是对半开，这也意味着其需要在没有符号位的情况下同时表示负数和正数。一个非常常见的处理手段就是所有数同时加上一个偏移量，这里这个偏移量就是127，此时所有表示都\(\geq 0\) 还是考虑小数10.75，其尾数的指数为3，加上偏移量之后为130,表示为01111000即可

最后得到10.75在FP32下表示为0 10000010 01011000...

误差的来源

观察IEEE-754标准，不难发现，尾数用于提供存储的精度，指数用于提供存储的范围。需要指出的是，在存储范围内，整数的表示是没有误差的，但是小数有。这是因为对于整数位，二进制表示本身就是一种准确无误差的表示，但是对于小数位，只能通过\(\sum \frac{1}{2^{k_{i}}}\)来不断拟合，而尾数所能表示的范围是有限的，也就意味着小数的拟合精度是受限的。

不过神奇的是，拟合精度带来的误差，并非是绝对误差，而是相对原数而言的。这一点是通过指数位实现的。

还是以FP32为例，其尾数有23位，那么拟合小数的时候，最高精度为\(\frac{1}{2^{23}}\approx 0.0000001192092896\)，这也意味着从小数点后第7位起，已经无法保证准确的拟合了。但是由于指数位的存在，如果原数的有效数字并不是从小数点后开始的话，可以通过指数位抹除中间多余的0，那么中间这几位的拟合精度将由指数位提供，那么最终拟合精度是大于7位的。 这一点可以通过0.123456789和0.00000123456789来理解。

同样的，对于FP16来说，其尾数为10，就始终可以相对提供约3-4位的十进制有效数字。

从而不难发现，IEEE-754标准保证的是固定位的十进制有效数字，但是这是相对于原数字来说的，与数值量级无关。

这一点可以通过程序看看

pi = math.pi
x = torch.tensor(pi, dtype = torch.float16)
y = torch.tensor(pi, dtype = torch.float32)
z = torch.tensor(pi, dtype = torch.float64)
print(f"pi: {pi}")  
print(f"FP16: {x}, {math.fabs(pi-x.item())}")
print(f"FP32: {y}, {math.fabs(pi-y.item())}")
print(f"FP64: {z}, {math.fabs(pi-z.item())}")

分别用FP16，FP32，FP64存储\(\text{pi}=\pi\)并输出，观察其结果与误差

不出意料，FP16可以保留2位有效精度，FP32可以保留6位有效精度。

而当我们将\(\text{pi}\)取做\(\pi \times 10^-2\)时，得到的结果为

此时FP16的有效精度就变成了4位，这是因为它的尾数实际拟合的依然是3.1415926...，多出来的两位精度由指数位提供了。 而FP32的有效精度也变成了8位，符合预期。

可以得到的另外一个有意思的结论就是 对于极小的数，其存储的绝对误差可能是更小的，比如存储1e-7和存储1e3的区别

总结

IEEE-754浮点标准下，浮点数存储存在精度误差，精度上限受到尾数位长度限制。

但是这里的误差是相对于有效数字的，不是绝对的小数点后位数，与数字量级无关。

FP16 始终相对提供约 3-4 位十进制有效数字，FP32始终相对提供约 6-7 位十进制有效数字，当然这里的“始终”也是建立在数字处于指数位表示范围内的前提下的。

当然，如果面对的是大规模随机数的存储，那么也只能将其精度直接估成小数点的有效数字了。