NOT ALL LLM-GENERATED DATA ARE EQUAL: RETHINKING DATA WEIGHTING IN TEXT CLASSIFICATION
现在LLM训练时会使用LLM产出的语料。但是LLM产出的分布与训练语料的分布往往会存在偏差,那么就会对训练带来影响。本文通过在CE loss中添加sample-wise的权重,调整不同样本对训练的贡献,来缓解这种分布的mismatch问题。
记\(P\)为真实世界数据分布,\(P'\)为从其中采样得到的一个子集(\(|P'|\approx 200\)),期望\(P'\)能够反映分布\(P\)。
\(Q\)为LLM产出的数据分布,\(\hat{P}\)为模型预测的分布,训练时的数据记为\(x\),其对应的label记为\(y\)。用\(Q\)中采样的数据\(D_{Q}\)进行训练的话,就有\(\{x,y\}\in D_{Q}\),可以将训练目标记为 \[ \mathbb{E}_{Q}[-\log \hat{P}(y|x;\theta)]\tag{1} \]
为了缓解上述问题,一个比较直观的想法是,对于那些\(P(y|x),Q(y|x)\)差距比较大的样本对\(\{x_{i,y_{i}}\}\),这意味着该样本偏离分布\(P\)的程度是比较大的,因此在loss中尝试投入更大的权重来修正,而那些\(P(y|x),Q(y|x)\)差距不算大的样本,可以投入相对小的权重。 重要性采样可以实现类似操作,也就是在\((1)\)式中插入\(P(y|x) / Q(y|x)\),得到训练目标为 \[ \mathbb{E}_{Q}\left[ -\frac{P(y|x)}{Q(y|x)} \log \hat{P}(y|x;\theta) \right]\tag{2} \] 这就充当了差距比较以及赋权重的角色。
想要得到分布\(P,Q\)的具体分布情况,就需要额外训两个model对其进行拟合。当然,分布\(P\)实际上也是不能直接拟合的,因此用分布\(\hat{P}\)进行近似,拟合得到的两个具体分布记为\(\hat{P}',\hat{Q}\),最终得到loss为 \[ L(\theta,D_{Q}) = -\frac{1}{N} \sum_{i=1}^{N} \frac{\hat{P}'(y_{i}|x_{i})}{\hat{Q}(y_{i}|x_{i})}\log \hat{P}(y_{i}|x_{i};\theta)\tag{3} \]
仔细观察这一式子,可以注意到在整个训练过程中,每一个样本所对应的权重其实是固定的,因此可以尝试根据训练状况为其赋以动态权重。
具体来说,由于训练数据来自\(D_{Q}\),从而分布\(\hat{P}\)本来就是在拟合\(Q\),其与\(\hat{Q}\)是类似的功能。因此将后者直接替换为\(\hat{P}(y_{i}|x_{i};\theta_{t})\),这里用\(\theta_{t}\)来强调其是随训练进行而不断变化的。\(\hat{P}'(y_{i}|x_{i})\)是拟合分布\(P'\)得到的,也可以选择将\(\hat{P}(y_{i}|x_{i};\theta_{t})\)过\(P'\)训一遍进行拟合,然后替换掉\(\hat{P}'(y_{i}|x_{i})\),最终得到loss为 \[ L_{\theta_{i},D_{Q}} = -\frac{1}{N} \sum_{i=1}^{N} \frac{\hat{P}(y_{i}|x_{i};\theta_{t},D_{P'})}{\hat{P}(y_{i}|x_{i};\theta_{t})}\log \hat{P}(y_{i}|x_{i};\theta_{t})\tag{4} \] 这里用\(\hat{P}(y_{i}|x_{i};\theta_{t},D_{P'})\)来代表\(\hat{P}(y_{i}|x_{i};\theta_{t})\)过一遍分布\(P'\)拟合之后的结果。
这种动态权重,按照个人理解,其实是在根据训练效果调整样本的权重了。预测结果与实际分布接近的话,权重会较大,反之则较大。也就是说,实际上与式\((3)\)的出发点已经不太一样了,并不是在根据分布P,Q的差距给权重。
另外,不管是式\((3)\)还是式\((4)\),对于那些在P中概率较小的样本,都没有很好的赋权策略。如果在P中某个样本对\(P(y_{i}|x_{i})\)比较小的话,训练得到的预测\(\hat{P}(y_{i}|x_{i};\theta)\)更有可能是偏大的,那么最终得到的权重反而是一个较小的值。
最后,对于式\((4)\)中的\(\hat{P}(y_{i}|x_{i};\theta_{t},D_{P'})\),用\(\hat{P}(\cdot;\theta_{t})\)再去拟合一遍\(P'\)是否有必要,直接用\((3)\)中的\(\hat{P}'(y|x)\)是否也是可以的?
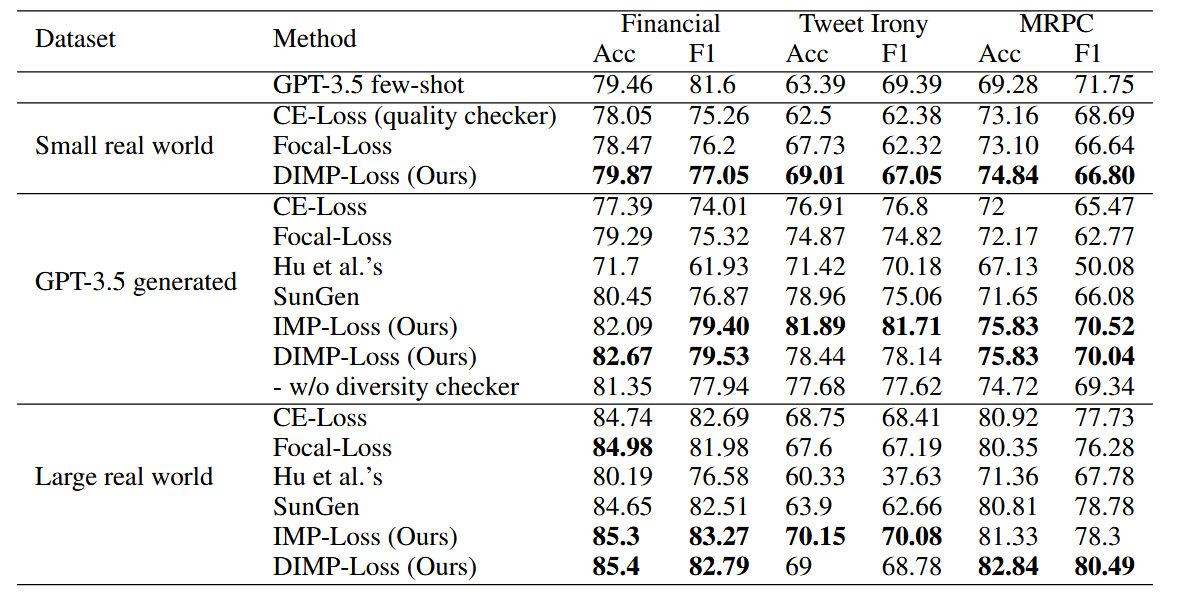
在最终的实验结果中,两种Loss并没有一方是有完全胜过另一方的,这或许也可以印证我的观点:两种loss其实是在从不同的角度进行加权,走的是两条路,\((4)\)并不能直接看成\((3)\)的改进。从缓解分布mismatch对训练影响的角度看,或许还是(3)更加合理一些。