Attention-Machanism
Attention Mechanism
现在给定一组数据,假设包含若干个 特征-值 对 \((Key,Value)\),那么现在我们拿着一个特征 \(Query\),要如何利用这组数据确定一个合理的\(value\)? 有一些比较naive的想法,比如取最近邻的对应\(Value\),或者取较近的几个\(Key\),再拿它们的\(Value\)做个平均啥的。这些想法有其合理性,并且都蕴含一个核心点就是: >我们在尽可能地将注意力集中在与\(Query\)相近的\(Key\)对应的\(Value\)上,因为这些\(Value\)更大概率会与我们要确定的值更加接近
所以就有了\(Attention\ Mechanism\)
低维
我们首先在一维空间\(\mathbb{R}\)下讨论这件事情。下面是一个非常直观的过程. 我们有若干组\((Key_i,Value_i)\),以及一个查询\(Query\),我们的目标是得到\(Output\).首先我们会让\(Query\)与各个\(Key_i\)做一个\(a\)运算,得到结果\(a(Query,Key_i)\),它表示\(Query\)与\(Key_i\)的相似程度,显然它与我们之后要在\(Key_i,Value_i\)上投入的注意力大小成正比,我们就记为注意力评分函数(attention scoring function).然后我们就拿\(a_i=a(Query,Key_i)\)转换成概率分布\(s_i\),再与\(Value_i\)相乘并求和得到 \[ Output = \sum_i s_iValue_i \] 这就是最后的结果了。 这里\(a_i\)到\(s_i\)我们简单点,可以直接取 \[ s_i=\frac{a_i}{\sum_{j=1}^{n} a_j} \] 可以看到这个求法还是有一定的合理性的,因为它不仅考虑到了注意力要偏向重点,还考虑到了整体的数据,而不是像之前那样只关注一小部分。接下来还剩下一个问题,就是我们的注意力评分函数\(a(Query,Key_i)\)要怎么算。一个方法就是可以使用核回归: 这里我们核函数选择\(Gauss\)核函数 \[ K(u)=\frac{1}{\sqrt{2\pi}}exp(-\frac{u^2}{2}) \] 从而\(u\)就取\(Query-Key_i\),得到 \[ Output = \sum_i\frac{exp(-\frac{1}{2}(Query-Key_i)^2)}{\sum_j exp(-\frac{1}{2}(Query-Key_j)^2)}Value_i \] 注意到第一个求和号里面其实就是一个softmax,从而 \[ Output = \sum_i softmax(-\frac{1}{2}(Query-Key_i)^2)Value_i \] 为了给整个模型加入一点可学习的东西,我们可以在softmax里面加入一个参数\(w\),得到 \[ Output = \sum_i softmax(-\frac{1}{2}(Query-Key_i)^2w)Value_i \] 这就是最终结果了。
高维
现在不管是\(Query,Key\)还是\(Value\),都从原本的一维数据变成了高维的向量,然后我们再重新审视这个问题。下面这张图是非常形象的。
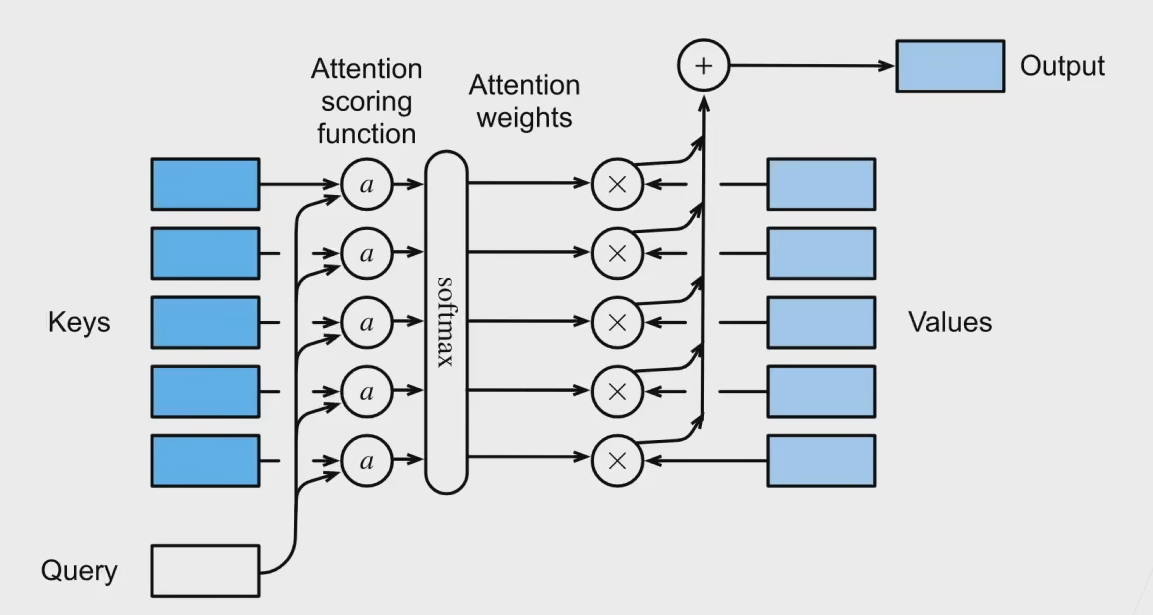 用一个函数\(f\)来形式化地描述整个过程。有\(n\)个键值对\(\boldsymbol{k_i}\in
\mathbb{R}^k,\boldsymbol{v_i}\in \mathbb{R}^v\),给定一个查询\(\boldsymbol{q}\in \mathbb{R}^q:\) \[
Output =
f(\boldsymbol{q},(\boldsymbol{k_1},\boldsymbol{v_1}),\cdots,(\boldsymbol{k_n},\boldsymbol{v_n}))=\sum_{i=1}^{n}\alpha(\boldsymbol{q},\boldsymbol{k_i})\boldsymbol{v_i}\in
\mathbb{R}^v
\] 其中 \[
\alpha(\boldsymbol{q,k_i})=\frac{exp(a(\boldsymbol{q,k_i}))}{\sum_{j=1}^{n}exp(a(\boldsymbol{q,k_j}))}
\]
由于把核函数的一部分抽象成了softmax操作,所以在低维情况下我们的\(a(q,k_i)\)函数实际对应的是\(-\frac{1}{2}(q-k_i)^2\)
而在高维向量情况下,我们有对\(a\)一般有两种处理方式
用一个函数\(f\)来形式化地描述整个过程。有\(n\)个键值对\(\boldsymbol{k_i}\in
\mathbb{R}^k,\boldsymbol{v_i}\in \mathbb{R}^v\),给定一个查询\(\boldsymbol{q}\in \mathbb{R}^q:\) \[
Output =
f(\boldsymbol{q},(\boldsymbol{k_1},\boldsymbol{v_1}),\cdots,(\boldsymbol{k_n},\boldsymbol{v_n}))=\sum_{i=1}^{n}\alpha(\boldsymbol{q},\boldsymbol{k_i})\boldsymbol{v_i}\in
\mathbb{R}^v
\] 其中 \[
\alpha(\boldsymbol{q,k_i})=\frac{exp(a(\boldsymbol{q,k_i}))}{\sum_{j=1}^{n}exp(a(\boldsymbol{q,k_j}))}
\]
由于把核函数的一部分抽象成了softmax操作,所以在低维情况下我们的\(a(q,k_i)\)函数实际对应的是\(-\frac{1}{2}(q-k_i)^2\)
而在高维向量情况下,我们有对\(a\)一般有两种处理方式
加性注意力
一般来说,当查询和键是不同长度的矢量时,可以使用加性注意力作为评分函数。此时给定\(\boldsymbol{q}\in \mathbb{R}^q,\boldsymbol{k}\in \mathbb{R}^k\),有 \[ a(\boldsymbol{q,k})=\boldsymbol{w}_v^T\ tanh(\boldsymbol{W}_q\boldsymbol{q+\boldsymbol{W}_k\boldsymbol{k}}) \] 其中\(\boldsymbol{W}_q\in \mathbb{R}^{h\times q},\boldsymbol{W}_k\in \mathbb{R}^{h\times k},\boldsymbol{w}_v\in \mathbb{R}^{h}\)都是可学习的参数,而\(h\)是作为一个可以调整的超参数,tanh就是一个激活函数。仔细观察一下就是,括号里面将\(\boldsymbol{q}\)和\(\boldsymbol{k}\)都转化成了一个\(h\)维向量,然后再与外面的\(\boldsymbol{w}_v^T\)一乘,就得到了一个实数作为最终结果
缩放点积注意力
当查询和键的长度相同时,我们就可以不必这么麻烦,把它们统一转化成一个长度的向量了。我们可以直接做向量内积,从而有\(\boldsymbol{q,k}\in \mathbb{R}^d\), \[ a(\boldsymbol{q},\boldsymbol{k})=\boldsymbol{q}^T\boldsymbol{k} \] 但是这样其实有一个问题。因为我们的结果\(a(\boldsymbol{q},\boldsymbol{k})\)是要拿去做softmax的,而softmax由于是由指数函数实现的,当指数差距过大时,概率的偏差就会变的极大,从而失去参考价值。所以我们可以统一除以一个\(\sqrt{d}\)来减少差距,至于为什么是\(\sqrt{d}\),我们在最后讨论一下
以上都是考虑样本数为1的情况,实际情况中有多个样本,多个数据,记为查询\(\boldsymbol{Q}\in \mathbb{R}^{m\times d}\),键值\(\boldsymbol{K}\in \mathbb{R}^{n\times d},\boldsymbol{V}\in \mathbb{R}^{n\times v}\),就有
\[
f=softmax(\frac{\boldsymbol{QK}^T}{\sqrt{d}})\boldsymbol{V}\in
\mathbb{R}^{m \times v}
\] 这里softmax操作就是对每一行进行softmax操作的意思
总体可以用这一张图表示 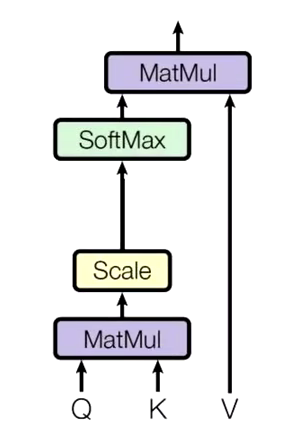 首先\(\boldsymbol{Q,K}\)做内积,然后放缩(除以\(\sqrt{d}\)),然后做softmax,最后与\(\boldsymbol{V}\)点乘
首先\(\boldsymbol{Q,K}\)做内积,然后放缩(除以\(\sqrt{d}\)),然后做softmax,最后与\(\boldsymbol{V}\)点乘
Self-Attention Mechanism
说是叫self-attention,不过我觉得这里的self更多的应该是指一个集合本身,而不是集合中的某一个元素 回忆一下Attention Mechanism:有\(m\)个长度为\(d\)的查询向量\(\boldsymbol{q_1,q_2,...q_n}\),就记为行向量好了,它们组成一个矩阵\(\boldsymbol{Q\in \mathbb{R}^{m\times d}}\),同理有n个键行向量组成的矩阵\(\boldsymbol{K}\in \mathbb{R}^{n\times d}\),以及\(n\)个值行向量组成的矩阵\(\boldsymbol{V}\in \mathbb{R}^{n\times v}\) >(这里为了方便我们就只讨论查询向量与键值向量的长度相等的情况了,然后就直接用Scaled Dot-Product Attention来处理了,另一种情况的处理显然也会是类似的)
然后就有结果矩阵 \[ f=softmax(\frac{\boldsymbol{QK}^T}{\sqrt{d}})\boldsymbol{V}\in \mathbb{R}^{m \times v} \] 这里有几点要指出: * f的行大小是与\(Q\)相同的,它相当于是对每一个询问行向量\(q_i\)的所有特征进行了一个回答 * 任意两个询问行向量\(q_i,q_j\)之间是可以没有任何关系的,相当于\(m\)次互不影响的询问 那么自注意力机制就是在次基础上做的改进 --- 我们现在有\(m\)个事物,它们是一个整体,\(m\)个事物之间有可能某个集合的事物之间是包含一定的关系的。如果我们想只用这\(m\)个事物的当前特征去做attention,得到一些信息,那么显然我们的查询矩阵\(\boldsymbol{Q}\)的每一行就要取对应事物的特征。那么\(\boldsymbol{K,V}\)呢?我们还是取这个集合内每一个事物的对应信息。相当于从集合内部的事物之间的隐含的关系来找到信息 从而我们的\(\boldsymbol{Q,K,V}\)的第\(i\)个行向量来自第\(i\)个事物的信息。为此我们需要引入\(\boldsymbol{W_q,W_k,W_v}\in \mathbb{R}^{d\times b}\)三个矩阵来提取信息,当然它们是可学习的,而这\(m\)个事物本身的信息可以写成一个\(\boldsymbol{X}\in \mathbb{R}^{m\times d}\),从而, \[ \boldsymbol{Q=XW_q,K=XW_k,V=XW_v} \] 最后套用原本的attention机制,我们得到 \[ f=softmax(\frac{\boldsymbol{QK}^T}{\sqrt{d}})\boldsymbol{V}\in \mathbb{R}^{m \times d} \] \(f\)的每一个行向量就是第\(i\)个事物从这n个事物当中提取到的信息了 注意到自注意力机制与普通的注意力机制的区别就在于:它的信息来源是一个固定的集合,集合的每一个元素既为其它元素提供信息,也从其它元素那里提取信息。所以我在这一节的一开始说,self更多的应该是指一个集合本身,而不是集合中的某一个元素 这样做的意义是:对于集合中的每一个元素\(a\),它可以从与它相近的其它元素中得到更多信息,而不仅仅是只有自己的信息
Multi-head Attention Mechanism
注意到之前对于每一个事物,我们只用了一组矩阵\(W_q,Q_k,Q_v\)来提取其特征。一个很自然的问题:这样提取够吗?会不会导致提取的信息不足? 解决方案也很简单,那就多用几组\(W_q,Q_k,Q_v\)来提取就好了,然后再把它们的结果放到一起,再拼在一起就可以啦。第\(i\)组用的矩阵就是\(W_{q_i},Q_{k_i},Q_{v_i}\),不同组之间显然是可以并行计算的,互不影响。
关于缩放系数\(\sqrt{d}\)
前面讲到了,attention操作最后需要做一个softmax,而softmax里面含有指数运算,如果数据的方差过大的话,最后得到的分布就会非常接近一个one hot分布,从而导致严重的梯度消失,为此我们需要对点积进行放缩。但是为什么放缩的系数是\(\sqrt{d}\)呢?(其中\(d\)是向量的长度)
我们考虑 \[ softmax(\frac{\boldsymbol{QK}^T}{\sqrt{d}})\boldsymbol{V}\in \mathbb{R}^{m \times v} \] 中的任意两个\(d\)维向量\(q,k\),假设它们采样自均值为0,方差为1的分布,那么它们内积的二阶矩为 \[ \begin{flalign} \mathbb{E}[(q\cdot k)^2] &= \mathbb{E}[(\sum_{i=1}^{d}q_ik_i)^2] = \mathbb{E}[(\sum_{i=1}^{d}q_ik_i)\cdot (\sum_{j=1}^{d}q_jk_j)]\\ &= \mathbb{E}[\sum_{i,j}^{d}(q_iq_j)(k_ik_j)]=\sum_{i,j}\mathbb{E}[q_iq_j]\mathbb{E}[k_ik_j] \\& =\sum_{i,j}\mathbb{E}[q_i]^2\mathbb{E}[k_i]^2 = d \end{flalign} \]
又\(\mathbb{E}[q\cdot k]^2=0\),从而\(\mathbb{V}ar[q\cdot k]=d\) 根据正态分布的3\(\sigma\)原则,我们不妨假定\(q\cdot k\)分布在\([-3\sqrt{d},3\sqrt{d}]\)中,那么在softmax中先做指数运算的时候,数据分布区间会变成\([e^{-3\sqrt{d}},e^{3\sqrt{d}}]\)中,一般来说\(d\)都是一个较大的值,从而左界会极小,右界又会极大,所以求梯度的时候很容易导致梯度消失,为此我们经验性地除上一个\(\sqrt{d}\),使得\(\mathbb{V}ar[q\cdot k]=1\),这会使得最后的区间大致分布在\([e^{-3},e^3]\),这是一个相对来说可以接受的区间,会有效缓解该问题,让网络能够更加稳定地更新。