Importance-Aware Data Selection for Efficient LLM Instruction Tuning
提出llm微调时的一种数据选择策略。利用In Context
Learning来判断模型在特定指令类型上的表现,从而能够有针对性地选择影响力高的数据。
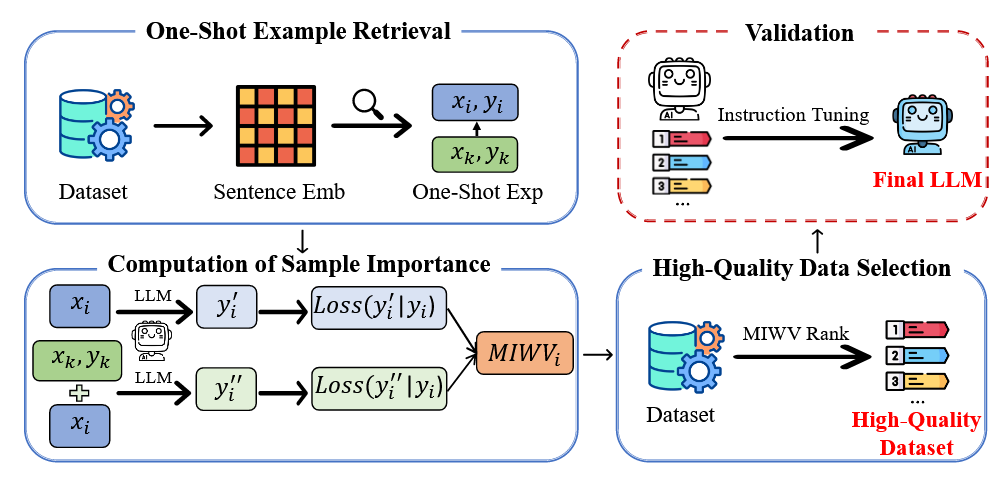
指令微调数据可以表示为\(\{(x_{1},y_{1}), (x_{2},y_{2}), \dots (x_{n}, y_{n})\}\),对于每一个\(x_{i} = (x_{i}^1, x_{i}^2, \dots x_{i}^Q)\),对每一个token做embedding操作,得到 \[ h_{i}^1, h_{i}^2, \dots h_{i}^Q = E(x_{i}^1, x_{i}^2, \dots x_{i}^Q) \] 这里\(E\)选择的模型是Bge-en-large。从而指令\(x_{i}\)的embedding结果为 \[ h_{i} = \frac{\sum_{q=1}^{Q}h_{i}^q}{Q} \] 之后用cos similarity找到与\(h_{i}\)最接近的\(h_{j}, j\neq i\),从而定义\((x_{j},y_{j})\)是\((x_{i}, y_{i})\)的one shot example
利用one shot example,我们可以定义数据的重要性: \[ MIWV(x_{i},y_{i}) = L_{\theta}(y_{i}|x_{i},C) - L_{\theta}(y_{i}|x_{i}) \] 其中\(C\)就是\((x_{i},y_{i})\)的one shot example。这里\(L_{\theta}(y_{i}|x_{i},C) = -\frac{1}{A}\sum_{a=1}^{A}\log p(y_{i}^{a}|x_{i},C,y_{i}^{<a})\)就是正常的CE Loss
之后取MIWV最高的\(k\%\)数据即可。这里MIWV越高,代表引入与construct类似的one shot example之后,模型的预测结果并没有多少提升,从而其在该数据上的学习更需要注重。 需要注意的是,有可能对于样本\((x_{i}, y_{i})\),其可能并没有非常接近的one shot example,引入的最接近的\((x_{j},y_{j})\)可能反而会阻碍模型预测。这种情况下,该样本的MIWV值也会比较高,从而被采样到,这在一定程度上也保证了训练数据的多样性。
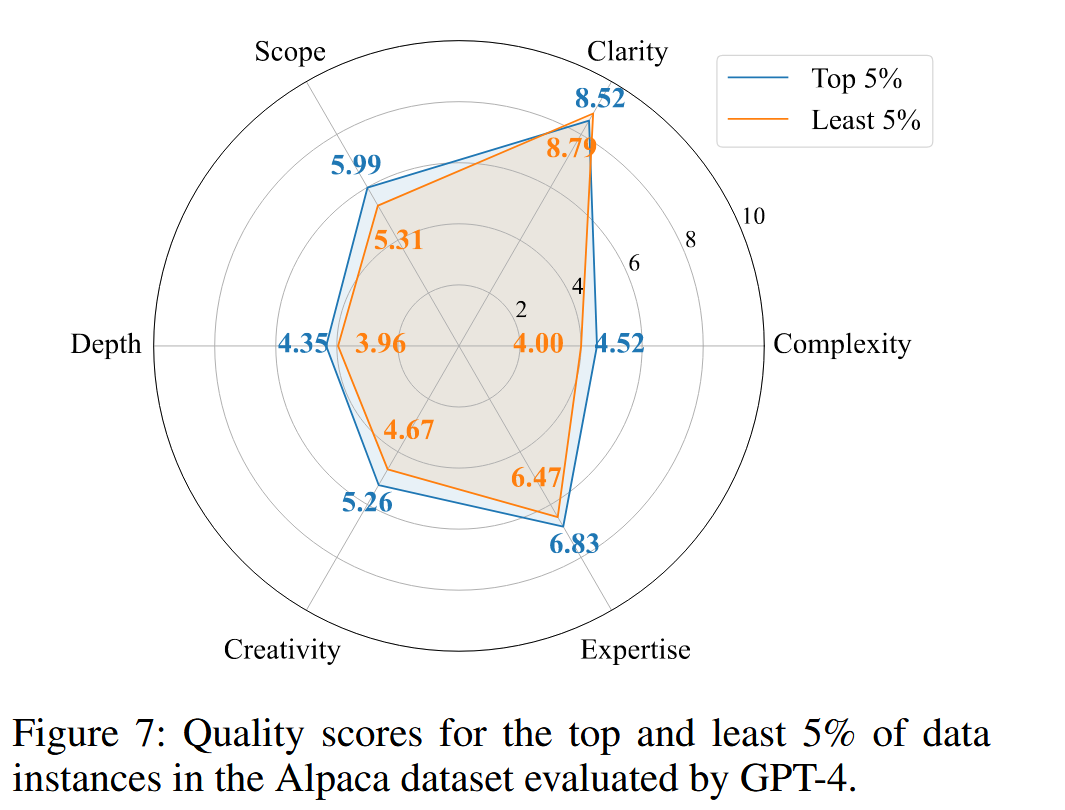
对数据质量的分析也表示,MIWVtop的样本,其分布质量往往会更好。
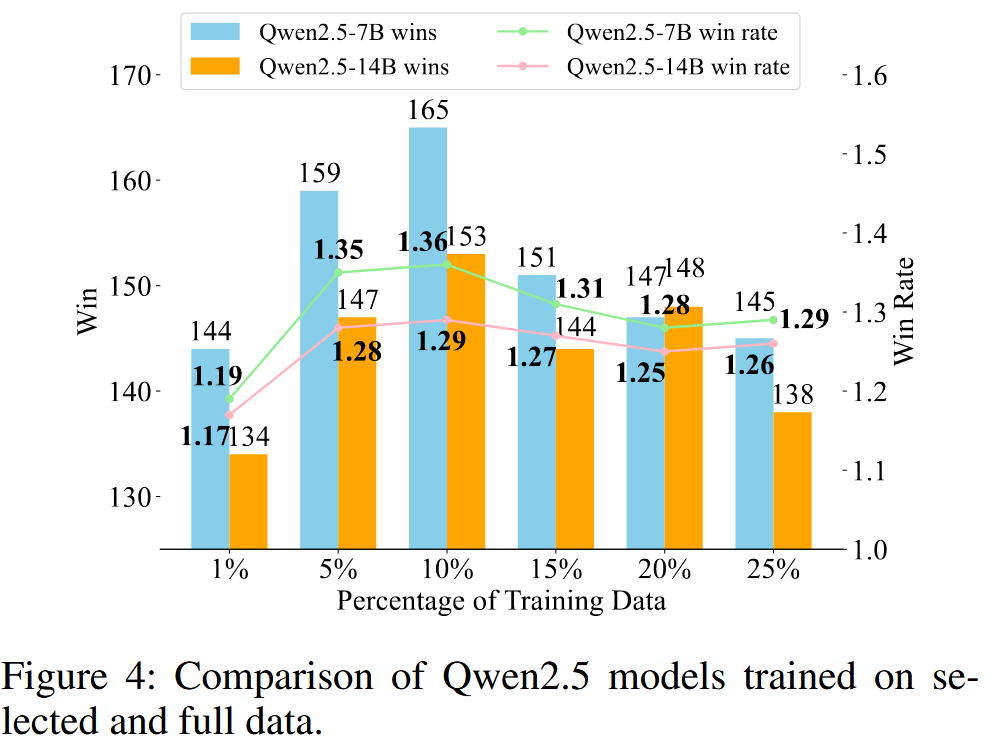
最后从实验结果上来看,哪怕仅仅使用前\(1\%\)的数据,训练效果也比使用全量数据要好,这也代表原始数据是冗余且存在噪声的。这里最优比例在\(15\%\)左右。