SGD收敛性学习笔记
之前就对sgd的看似无脑的贪心策略感到十分新奇,为什么每次随机用一个子集的梯度来更新就可以近似整体的梯度? 正好最近重新实现了一遍sgd,就顺便补一下它的理论证明。
准备工作
不妨假设我们模型的损失函数为\(L(x,\theta)\),其中\(x\)是训练数据,\(\theta\in R^d\)是模型参数,一般来说我们优化的目标是找到最优的\(\theta^*\)使得\(L(x,\theta^*)\)最小,也就是 \[ \theta^* = argmin_{\theta\in R^d} L(x,\theta) \] 随机梯度下降(SGD)的策略是每次随机取数据\(x\)的一个子集,我们不妨将第\(t\)次取出的子集记为\(x^t\),那么更新方式为 \[ \theta^{t+1} = \theta^t - \eta^tg(x^t,\theta^t) \] 其中\(\eta^t\)表示第\(t\)次更新的学习率,\(g(x^t,\theta^t) = \nabla_\theta L(x^t,\theta)\)表示损失函数关于参数\(\theta\)的梯度。
我们当然可以直接写出\(\theta^t\)的通项为 \[ \theta^t = \theta^1-\sum_{s=1}^{t-1} \eta^sg(x^s,\theta^s) \] 当然这么看的话似乎很难说明参数\(\theta\)会收敛,更别说收敛到\(\theta^*\)了。所以我们尝试制定一个评价指标。
那么我们要如何评价这个策略?一个比较合理的目标是最小化 \[ L(T) = \frac{1}{T}\sum_{t=1}^{T}L(x^t,\theta^t) \] 其中\(T\)表示我们的迭代总轮数
又注意到\(L(T)\)的最小值我们可以表示为\(L(T)' = \frac{1}{T}\sum_{t=1}^{T}L(x^t,\theta^*)\) 那么我们的评价指标可以选择为 \[ \frac{1}{T}\sum_{t=1}^{T}L(x^t,\theta^t)-\frac{1}{T}\sum_{t=1}^{T}L(x^t,\theta^*)=\frac{1}{T}R(T)\ \ \ \ \ \ (1) \] 其中 \[ R(T)=\sum_{t=1}^{T}L(x^t,\theta^t)-\sum_{t=1}^{T}L(x^t,\theta^*) \] 被称为"regret"
当 \[ \lim_{T\rightarrow \infty}\frac{1}{T}R(T)=0 \] 时,我们就可以说这个策略确实是收敛的,参数\(\theta\rightarrow \theta^*\),也就是说,它不仅收敛,而且收敛于最优参数\(\theta^*\)
证明过程
现在我们考虑对\((1)\)式的收敛性进行证明。不过在此之前,我们需要假设对于任意的\(t,x^t\),损失函数\(L(x^t,\theta)\)都是关于\(\theta\)的convex函数,也就是说,\(\forall \theta^i,\theta^j\),都有 \[ L(x^t,\theta^i)-L(x^t,\theta^j)\geq (\theta^i-\theta^j)\cdot g(x^t,\theta^j)\ \ \ \ \ (2) \] 其中\(\cdot\)表示向量内积
现在我们就可以正式开始证明了!
想要证明\((1)\)式收敛于0,一个常见的办法就是为其找一个关于\(T\)的上界\(f(T)\),如果\(f(T)\rightarrow 0,T\rightarrow \infty\)的话,结论就得证了。
利用\((2)\)式,我们现在就能为\(R(T)\)找一个上界 \[ \begin{flalign} R(T)&=\sum_{t=1}^{T}L(x^t,\theta^t)-\sum_{t=1}^{T}L(x^t,\theta^*)\\ &=\sum_{t=1}^{T}(L(x^t,\theta^t)-L(x^t,\theta^*))\\ &\leq \sum_{t=1}^{T}(\theta^t-\theta^*)\cdot g(x^t,\theta^t) \end{flalign} \] 最后一个不等号由\((2)\)式变形之后即得
为了后面方便区分内积与数乘,我们将上式重新表述如下 \[ R(T)\leq \sum_{t=1}^{T}\left \langle \theta^t-\theta^*,g(x^t,\theta^t) \right \rangle \ \ \ \ \ (3) \] 接下来尝试为不等式右端找到替代,这一点可以从SGD的迭代公式出发 \[ \begin{flalign} \theta^{t+1} &= \theta^t - \eta^tg(x^t,\theta^t)\\ \theta^{t+1}-\theta^* &= \theta^t-\theta^*-\eta^tg(x^t,\theta^t)\\ \left \| \theta^{t+1}-\theta^* \right \|^2 &= \left \| \theta^t-\theta^*-\eta^tg(x^t,\theta^t) \right \|^2 \\ \left \| \theta^{t+1}-\theta^* \right \|^2 &= \left \| \theta^{t}-\theta^* \right \|^2 +(\eta^t)^2 \left \| g(x^t,\theta^t) \right \|^2 -2\eta^t \left \langle \theta^t-\theta^*,\eta^tg(x^t,\theta^t) \right \rangle\\ \end{flalign} \] 从而 \[ \left \langle \theta^t-\theta^*,\eta^tg(x^t,\theta^t) \right \rangle = \frac{1}{2\eta^t} \left [ \left \| \theta^{t}-\theta^* \right \|^2 -\left \| \theta^{t+1}-\theta^* \right \|^2 \right ] + \frac{\eta^t}{2} \left \| g(x^t,\theta^t) \right \|^2 \] 代入\((3)\)式,我们就有 \[ R(T)\leq \underbrace{\sum_{t=1}^{T} \frac{1}{2\eta^t} \left [ \left \| \theta^{t}-\theta^* \right \|^2 -\left \| \theta^{t+1}-\theta^* \right \|^2 \right ] }_{(a)}+ \underbrace{\sum_{t=1}^{T} \frac{\eta^t}{2} \left \| g(x^t,\theta^t) \right \|^2}_{(b)} \] 我们先来看第一部分\((a)\) \[ \begin{flalign} (a) &= \sum_{t=1}^{T} \frac{1}{2\eta^t} \left [ \left \| \theta^{t}-\theta^* \right \|^2 -\left \| \theta^{t+1}-\theta^* \right \|^2 \right ]\\ &= \frac{1}{2\eta^1} \left [ \left \| \theta^{1}-\theta^* \right \|^2 -\left \| \theta^{2}-\theta^* \right \|^2 \right ] + ... + \frac{1}{2\eta^T} \left [ \left \| \theta^{T}-\theta^* \right \|^2 -\left \| \theta^{T+1}-\theta^* \right \|^2 \right ]\\ &= \frac{1}{2\eta^1}\left \| \theta^{1}-\theta^* \right \|^2-\frac{1}{2\eta^T}\left \| \theta^{T+1}-\theta^* \right \|^2 + \sum_{t=2}^{T} \left \| \theta^{t}-\theta^* \right \|^2(\frac{1}{2\eta^t}-\frac{1}{2\eta^{t-1}}) \end{flalign} \] 这里我们还需要添加几个假设
- \(\eta_t\)序列是单调不递增的,即\(\eta^{t+1}\geq \eta^t,\forall t\geq 1\)
- \(D = max\{\left \| \theta^{t}-\theta^* \right \|\}<\infty\)
第一点其实比较好理解,因为我们在实际训练的过程中也是保证学习率逐渐变小的,第二点在大部分情况下其实也是成立的。
从而 \[ \begin{flalign} (a)&\leq \frac{1}{2\eta^1}D^2 + \sum_{t=2}^{T} D^2(\frac{1}{2\eta^t}-\frac{1}{2\eta^{t-1}})\\ &=\frac{1}{2\eta^1}D^2 + D^2(\frac{1}{2\eta^T}-\frac{1}{2\eta^{1}})\\ &= \frac{D^2}{2\eta^T} \end{flalign} \] 再来看看第二部分 \[ (b) = \sum_{t=1}^{T} \frac{\eta^t}{2} \left \| g(x^t,\theta^t) \right \|^2 \] 我们做与上一部分类似的假设 \[ G = max{\left \| g(x^t,\theta^t) \right \|^2}<\infty \] 从而 \[ (b)\leq \sum_{t=1}^{T}\frac{G^2}{2}\eta^t = \frac{G^2}{2}\sum_{t=1}^{T}\eta^t \] 最终我们得到下式 \[ R(T)=\sum_{t=1}^{T}L(x^t,\theta^t)-\sum_{t=1}^{T}L(x^t,\theta^*)\leq \frac{D^2}{2\eta^T} + \frac{G^2}{2}\sum_{t=1}^{T}\eta^t\ \ \ \ \ (4) \] 如果我们将上界取高的话,\(D,G\)完全可以视作常数,从而右式就是一个只跟学习率\(\eta^t\)有关的式子了
我们没能做到一开始期望的将右式处理成只跟T有关,事实上这也不太现实。不过只跟\(\eta^t\)有关的话,这也意味着只要我们的学习率策略取的足够好,使得右式关于T的最高阶小于1,那么SGD的收敛性就还是存在的。
例如,如果我们取学习率为\(C\cdot t^{-1/2}\),其中\(C>0\)为常数,那么 \[ \begin{flalign} R(T)&\leq \frac{D^2\sqrt{T}}{2C} + \frac{CG^2}{2}\sum_{t=1}^{T}\frac{1}{\sqrt{t}}\\ &\leq \frac{D^2\sqrt{T}}{2C} + \frac{CG^2}{2}\sum_{t=1}^{T}\frac{2}{\sqrt{t-1}+\sqrt{t}}\\ &\leq \frac{D^2\sqrt{T}}{2C} + \frac{CG^2}{2}\sum_{t=1}^{T}2(\sqrt{t}-\sqrt{t-1})\\ &\leq \frac{D^2\sqrt{T}}{2C} + CG^2\sqrt{T} \end{flalign} \] 从而 \[ \frac{1}{T}R(T) \leq \frac{D^2}{2C\sqrt{T}} + \frac{CG^2}{\sqrt{T}} \]
而如果将学习率取为常数\(\eta\)的话,\((4)\)式右端为 \[ \frac{D^2}{2\eta^T} + \frac{G^2}{2}\sum_{t=1}^{T}\eta^t = \frac{D^2}{2\eta} + \frac{G^2}{2}T\eta\geq \frac{DG\sqrt{T}}{2} \] 从而当学习率\(\eta\)取为\(\frac{D}{D\sqrt{T}}\)时,有 \[ \frac{1}{T}R(T)\leq \frac{DG}{2\sqrt{T}} \] 可以看到两者都是\(O(\frac{1}{\sqrt{T}})\)级别的,当\(T\rightarrow \infty\)时,都是能收敛的。
当然我们也能看出来,当学习率取的不好的时候,\(R(T)\)的上界可能会非常松,那么所谓收敛性也就无从谈起了。
实验
\((4)\)式与学习率的关系如此紧密,这也难怪SGD这种方法会对超参数如此敏感。本人简单做了一个不同学习率下的对比实验,学习率都设置为常数,可以看到不同情况下loss的下降曲线差异也是很大的。
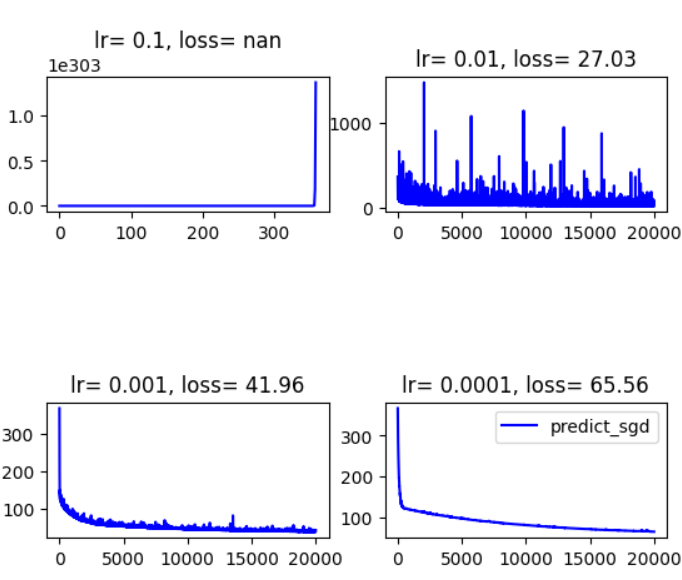
同时做了另一组,学习率取为\(Ct^{-1/2}\),结果为
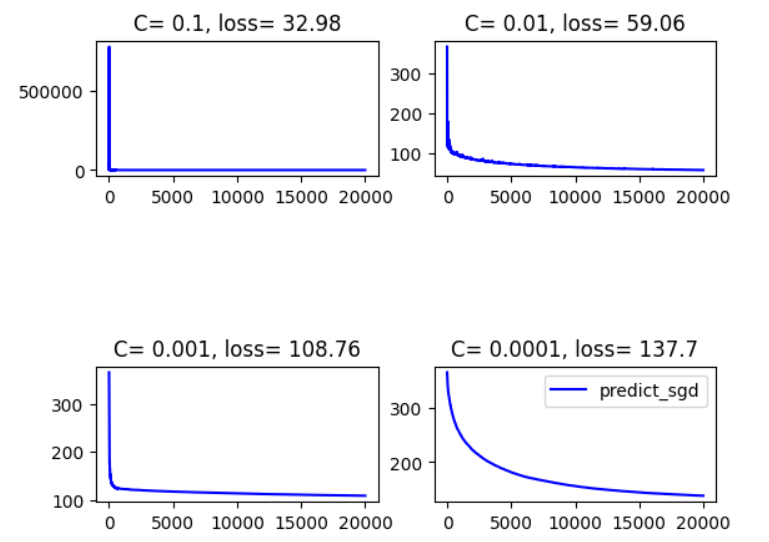
可以看到学习率取常数的话,最终的loss普遍是要比取\(Ct^{-1/2}\)要好的,这一点从上面的分析中也许可以解释一下:前者的理论上界为\(\frac{DG}{2\sqrt{T}}\),而后者的理论上界为\(\frac{D^2}{2C\sqrt{T}} + \frac{CG^2}{\sqrt{T}}\),是要更大的
但是取常数貌似受随机性的影响会更大
以及学习率如果过小的话,loss下降速度也会受到影响,对应的最终的loss仿佛也会偏高。
以上是笔者作为初学者的一些探究,或许在之后的学习过程中能找到更加合理的解释。如果文章有错误的话也欢迎指教。
总结
我们证明了SGD在一定的假设下确实可以收敛,这些假设为:
- 损失函数\(L(x^t,\theta^t),\forall t\geq 1\)关于\(\theta\)是convex函数
- 学习率\(\eta_t\)序列是单调不递增的,即\(\eta^{t+1}\geq \eta^t,\forall t\geq 1\),非常合理
- \(D = max\{\left \| \theta^{t}-\theta^* \right \|\}<\infty\),实际上它要求参数位于线性空间的一个有界集合内
- \(G = max{\left \| g(x^t,\theta^t) \right \|^2}<\infty\),也就是梯度有界
其余诸如损失函数可导等条件略过。
证明的重要一环便是\((1)\)式 \[ \frac{1}{T}\sum_{t=1}^{T}L(x^t,\theta^t)-\frac{1}{T}\sum_{t=1}^{T}L(x^t,\theta^*)=\frac{1}{T}R(T) \] 它衡量了实际迭代过程与理论最优过程的差距,在学习率的选择上我们或许也可以以最小化这个式子的理论上界为目标。当然这只是加了很多假设的理论分析,实操不见得有效。
最终得到在给定假设下上式的理论上界为 \[ \frac{1}{T}R(T)=\sum_{t=1}^{T}\frac{1}{T}L(x^t,\theta^t)-\frac{1}{T}\sum_{t=1}^{T}L(x^t,\theta^*)\leq \frac{D^2}{2T\eta^T} + \frac{G^2}{2T}\sum_{t=1}^{T}\eta^t \] 感觉还是很有收获的!
参考文献
[1] M. Zinkevich, “Online convex programming and generalized infinitesimal gradient ascent,” in Proceedings of the 20th international conference on machine learning (ICML-03), 2003, pp. 928– 936.