二分图博弈学习笔记

二分图博弈

二分图博弈是少有的直接跟图论挂钩的一种博弈模型

一个博弈是二分图博弈应当满足一下条件：

  • 博弈人数为两人，轮流操作
  • 博弈状态转移可以表示成一张二分图
  • 不可访问已经访问过的状态
  • 无法转移者负

拥有二分图这么良好的性质，该博弈模型自然而然的有一个很简单的结论：如果先手状态，我们记为P，一定在二分图的最大匹配中，那么先手必胜。否则先手必败。

那么我们来看看证明：

假设当前P不在最大匹配中，那么先手移动之后P一定会到达一个匹配点，否则我们就有了一个新的匹配，与最大匹配这一点矛盾。所以此时我们的局面是当前处于匹配点上，后手先行动。后手走的下一个点也一定是匹配点，否则就跟之前的路径形成了一条增广路，同样矛盾。所以接下来双方都是在匹配点上转移。显然最终移动步数为偶数，故此时后手必胜。

若P在最大匹配中，则只要仿照上述策略，就是一个必胜的局面。

如果P没有可以转移的局面，同样也是不在最大匹配中，当然也是必败。

由此，对于一个二分图博弈，只要我们能够判断先手所在局面是否处在二分图的最大匹配上，即可判断必胜状态。

如何判断一个点是否一定在最大匹配上？比较经典的套路就是先将其从图中移除，然后再加进来，看看是否还能对匹配有贡献。如果有的话，说明其一定处在最大匹配上。

具体实现，我们可以采用网络流。在建图的时候先不将P与源点或者汇点连接，这样跑网络流的时候就不会将其考虑进去。然后把P与源点/汇点连接，利用残量网络，再做一遍网络流。如果值非0，就是有贡献的。

但是该方法仅适用于单起点博弈 。如果需要判断的局面过多，显然时间复杂度无法接受。

如果想要找出所有局面中的必胜局面，我们有更好的办法。

找出所有必胜局面，也就是找出所有一定处在最大匹配的点，相当于找出所有不一定在最大匹配上的点。

img

点击并拖拽以移动编辑

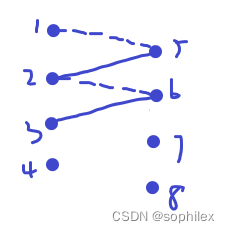
非匹配边1->5和2->5匹配边可以互换最大匹配数不变，所以点1,2都不一定在最大匹配中。在该图的残量网络中，1->5的流量为1，匹配边5->2的反向流量为1，因此我们判断两条边可以互换。将与源点相连的边颜色col设为1，汇点设为0，dfs即可。这是判断与左部点的，判断右部点同理。

但是，但是，并不是所有满足二分图博弈模型的题目都一定得通过网络流来求解，因为不同博弈模型本身有其独特的性质，可能可以通过其他途径求解，比如*23牛客多校2 I Link with Gomoku*

然后就到了喜闻乐见的例题时间

[COCI2017-2018#5] Planinarenje

大意： img点击并拖拽以移动​

模板题

不难发现，判负的条件与一方无法行动是等价的，所以该问题完美符合二分图博弈模型。然后又因为要对所有先手局面判断是否必胜，那么我们应该采用第二种方法。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
const ll maxn=2e5+10,maxm=2e5+10;
const ll inf=0x3f3f3f3f;
struct MaximumFlow
{
    //maxn 最多点数 maxm 最多边数
    int h[maxn],e[maxm],ne[maxm],f[maxm],idx;
    int d[maxn],cur[maxn];
    int n,m,S,T,mxn;
    ll col[maxn],ans[maxn];
    ll flag=0;
    void init(int n,int _s,int _t)
    {
        mxn=n,idx=0,S=_s,T=_t;//mxn表示最大点的大小（包括S，T），用于初始化处理，_s表示源点，_T表示汇点
        // memset(h,-1,sizeof h);
        while(n>=0)
            h[n--]=-1;
    }
    void addedge(int a,int b,int c)
    {
        ne[idx]=h[a],e[idx]=b,f[idx]=c,h[a]=idx++;
        ne[idx]=h[b],e[idx]=a,f[idx]=0,h[b]=idx++;
    }
    bool bfs()
    {
        // memset(d,-1,sizeof d);
        for(int i=0;i<=mxn;++i) d[i]=-1;
        d[S]=0;
        queue<int>q;
        q.push(S);
        cur[S]=h[S];
        while(q.size())
        {
            int t=q.front();
            q.pop();
            for(int i=h[t];i!=-1;i=ne[i])
            {
                int j=e[i];
                if(d[j]==-1&&f[i])
                {
                    d[j]=d[t]+1;
                    cur[j]=h[j];
                    if(j==T)return true;
                    q.push(j);
                }
            }
        }
        return false;
    }
    int find(int u,int limit)
    {
        if(u==T)return limit;
        int flow=0;
        for(int i=cur[u];i!=-1&&flow<limit;i=ne[i])
        {
            cur[u]=i;
            int j=e[i];
            if(d[j]==d[u]+1&&f[i])
            {
                int t=find(j,min(f[i],limit-flow));
                if(!t)d[j]=-1;
                f[i]-=t,f[i^1]+=t,flow+=t;
            }
        }
        return flow;
    }
    int dinic()
    {
        int r=0,flow;
        while(bfs())while(flow=find(S,inf))r+=flow;
        return r;
    }
    void dfs(int u,int t)
    {
        // vis[u]=1;
        if(col[u]==t)
        {
            flag=1;
            ans[u]=1;
        }
        for(int i=h[u];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(f[i]==t&&!ans[j])
            {
                dfs(j,t);
            }
        }
    }
    ll judge()
    {
        dinic();
        dfs(S,1);dfs(T,0);
        return flag;
    }

}f;
ll n,m;
ll S,T;
ll a,b;
void solve()
{
    cin>>n>>m;
    S=n*2+1;T=n*2+2;
    f.init(T+1,S,T);
    while(m--)
    {
        cin>>a>>b;
        f.addedge(a,b+n,1);
    }
    for(int i=1;i<=n;++i)
    {
        f.addedge(S,i,1);
        f.col[i]=1;
        f.addedge(i+n,T,1);
    }
    f.judge();
    for(int i=1;i<=n;++i)
    {
        if(f.ans[i]==0) cout<<"Slavko"<<endl;
        else cout<<"Mirko"<<endl;
    }

}
int main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    solve();
    return 0;
}
点击并拖拽以移动

20ccpc长春H

大意： 有m个数位的数字锁，存在若干状态不允许访问，也不允许访问之前访问过的节点，每次操作改变某一位，无法操作者负。给定锁的初始状态，问必胜状态。

思路： 显然锁的状态是一张二分图，因为数位和奇偶性相同的状态显然无法一次到达。那么我们只要把非法的状态不加入图中，然后采用第一种判断方法就可以了。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
#include<bits/stdc++.h>
using namespace std;
#define ll int
const ll INF=1e8;
const ll inf=1e8;
const int maxn=1e6+10,maxm=9e6+10;
const ll N=1e6+10;


struct MaximumFlow
{

    int h[maxn],e[maxm],ne[maxm],f[maxm],idx;
    int d[N],cur[N];
    int n,m,S,T,mxn;
    void init(int n,int _s,int _t)
    {
        mxn=n,idx=0,S=_s,T=_t;
        // memset(h,-1,sizeof h);
        while(n>=0)h[n--]=-1;
    }
    void addedge(int a,int b,int c)
    {
        ne[idx]=h[a],e[idx]=b,f[idx]=c,h[a]=idx++;
        ne[idx]=h[b],e[idx]=a,f[idx]=0,h[b]=idx++;
    }
    bool bfs()
    {
        memset(d,-1,sizeof d);
        d[S]=0;
        queue<int>q;
        q.push(S);
        cur[S]=h[S];
        while(q.size())
        {
            int t=q.front();
            q.pop();
            for(int i=h[t];i!=-1;i=ne[i])
            {
                int j=e[i];
                if(d[j]==-1&&f[i])
                {
                    d[j]=d[t]+1;
                    cur[j]=h[j];
                    if(j==T)return true;
                    q.push(j);
                }
            }
        }
        return false;
    }
    int find(int u,int limit)
    {
        if(u==T)return limit;
        int flow=0;
        for(int i=cur[u];i!=-1&&flow<limit;i=ne[i])
        {
            cur[u]=i;
            int j=e[i];
            if(d[j]==d[u]+1&&f[i])
            {
                int t=find(j,min(f[i],limit-flow));
                if(!t)d[j]=-1;
                f[i]-=t,f[i^1]+=t,flow+=t;
            }
        }
        return flow;
    }
    int dinic()
    {
        int r=0,flow;
        while(bfs())while(flow=find(S,inf))r+=flow;
        return r;
    }
}f;
ll n,m,pwd;
ll vis[N];
ll c[]={1,10,100,1000,10000,100000};
ll gt(ll x)
{
    ll sum=0;
    while(x)
    {
        sum+=x%10;
        x/=10;
    }
    return sum%2;
}
void solve()
{
    cin>>m>>n>>pwd;
    memset(vis,0,sizeof vis);
    for(int i=1;i<=n;++i)
    {
        ll a;cin>>a;vis[a]=1;
    }
    ll up=1;for(int i=1;i<=m;++i) up*=10;
    ll S=up,T=up+1;
    f.init(up+5,S,T);
    for(int i=0;i<up;++i)
    {
        //判断pwd是否一定在二分图的最大匹配中，一开始不将其与S或T连边
        //但是与网络其他节点相连。跑完网络流之后将pwd与对应起点/终点相连。
        //利用残量网络再跑一遍网络流。如果值大于0，代表其一定在二分图的最大匹配中
        if(vis[i]) continue;
        if(gt(i))
        {
            if(i!=pwd) f.addedge(i,T,1);
            continue;
        }
        if(i!=pwd) f.addedge(S,i,1);

        ll x;
        for(int j=0;j<m;++j)
        {
            x=i;
            int num=i;
            x/=c[j];
            x%=10;
            num=num-x*c[j];
            ll t1=num+((x+1)%10)*c[j];
            f.addedge(i,t1,1);
            t1=num+((x-1+10)%10)*c[j];
            f.addedge(i,t1,1);
        }
    }
    f.dinic();
    if(gt(pwd)) f.addedge(pwd,T,1);
    else f.addedge(S,pwd,1);
    if(f.dinic()) cout<<"Alice"<<endl;
    else cout<<"Bob"<<endl;
}
int main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    ll t;cin>>t;while(t--)
    solve();
    return 0;
}
点击并拖拽以移动

[NOI2011] 兔兔与蛋蛋游戏

大意：

n行m列的棋盘，每一格有一个黑/白棋，还有一个位置是空的

每一局游戏总是兔兔先操作，之后双方轮流操作，具体操作为：

  • 兔兔每次操作时，选择一枚与空格相邻的白色棋子，将它移进空格。
  • 蛋蛋每次操作时，选择一枚与空格相邻的黑色棋子，将它移进空格。

第一个不能按照规则操作的人输掉游戏。

思路： 有幸做出人生第二道黑题（敲下来有阻塞，但没想象中那么费劲）

我们稍微转化一下，将黑白棋的移动看成空格的移动。先手操作的时候，空格只能与白棋交换，此空格相当于黑棋。后手操作的时候，空格只能与黑棋交换，此时空格相当于白棋。所以相当于轮流在黑白棋之间切换，每次只能与不同颜色的点交换位置，显然是一张二分图。此外有一个性质比较隐蔽，那就是我们无法访问之前访问过的局面。因为黑白棋是轮流操作的，黑棋走过的点白棋是无法走的，反之同理。由此，我们成功转化成了二分图博弈，

这题要求我们输出所有操作失误的步骤。其实就是操作前后的都处于必胜状态的点。（仔细想想，不难理解）。每次操作之后整张图都不一样了，我们要判断的起始点也不一样了，所以我们每次要重新建图，因为图比较小，所以该方法是可行的。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=110;
const ll INF=0x3f3f3f3f,inf=INF;
const ll maxn=4000,maxm=maxn*20;
struct MaximumFlow
{
    //maxn 最多点数 maxm 最多边数
    int h[maxn],e[maxm],ne[maxm],f[maxm],idx;
    int d[maxn],cur[maxn];
    int n,m,S,T,mxn;
    ll mp_vis[maxn];
    ll col[maxn],ans[maxn];
    ll flag=0;
    void init(int n,int _s,int _t)
    {
        mxn=n,idx=0,S=_s,T=_t;//mxn表示最大点的大小（包括S，T），用于初始化处理，_s表示源点，_T表示汇点
        // memset(h,-1,sizeof h);
        while(n>=0)
            h[n--]=-1;
    }
    void addedge(int a,int b,int c)
    {
        ne[idx]=h[a],e[idx]=b,f[idx]=c,h[a]=idx++;
        ne[idx]=h[b],e[idx]=a,f[idx]=0,h[b]=idx++;
    }
    bool bfs()
    {
        // memset(d,-1,sizeof d);
        for(int i=0;i<=mxn;++i) d[i]=-1;
        d[S]=0;
        queue<int>q;
        q.push(S);
        cur[S]=h[S];
        while(q.size())
        {
            int t=q.front();
            q.pop();
            for(int i=h[t];i!=-1;i=ne[i])
            {
                int j=e[i];
                if(d[j]==-1&&f[i])
                {
                    d[j]=d[t]+1;
                    cur[j]=h[j];
                    if(j==T)return true;
                    q.push(j);
                }
            }
        }
        return false;
    }
    int find(int u,int limit)
    {
        if(u==T)return limit;
        int flow=0;
        for(int i=cur[u];i!=-1&&flow<limit;i=ne[i])
        {
            cur[u]=i;
            int j=e[i];
            if(d[j]==d[u]+1&&f[i])
            {
                int t=find(j,min(f[i],limit-flow));
                if(!t)d[j]=-1;
                f[i]-=t,f[i^1]+=t,flow+=t;
            }
        }
        return flow;
    }
    int dinic()
    {
        int r=0,flow;
        while(bfs())while(flow=find(S,inf))r+=flow;
        return r;
    }
    bool judge(ll x,ll y)
    {
        for(int i=h[x];i!=-1;i=ne[i])
        {
            ll Y=e[i];
            if(Y==y) return 1;
        }
        return 0;
    }
}f;
ll n,m;
char mp[N][N];
ll px,py;
ll S,T;
vector<ll> ans;
ll gt(ll x,ll y)
{
    return y+(x-1)*m;
}
ll dir[][4]={{1,0},{-1,0},{0,1},{0,-1}};
bool inmap(ll x,ll y)
{
    return x>=1&&y>=1&&x<=n&&y<=m;
}
bool jd(ll x,ll y)
{
    if(x==px&&y==py) return 1;//是当前操作点
    return 0;
}
inline ll gt()
{
    //奇数点与汇点相连
    //偶数点与源点相连
    f.init(n*m+5,S,T);//每次要将起始点与源点/汇点断开连接，重新建图，反正图也不大
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=m;++j)
        {
            if(jd(i,j)) continue;//去掉操作起始点
            if((i+j)%2==0) continue;
            f.addedge(gt(i,j),T,1);
        }
    }
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=m;++j)
        {
            if((i+j)%2) continue;//去掉操作起始点
            if(!jd(i,j)) f.addedge(S,gt(i,j),1);
            for(int k=0;k<4;++k)
            {
                ll xx=i+dir[k][0];
                ll yy=j+dir[k][1];
                if(!inmap(xx,yy)) continue;
                if(mp[xx][yy]==mp[i][j]) continue;
                f.addedge(gt(i,j),gt(xx,yy),1);
            }
        }
    }
    f.dinic();
    if((px+py)%2) f.addedge(gt(px,py),T,1);
    else f.addedge(S,gt(px,py),1);

    return f.dinic();
}

void solve()
{
    cin>>n>>m;
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=m;++j)
        {
            cin>>mp[i][j];
            if(mp[i][j]=='.')
            {
                px=i;py=j;
            }
        }
    }
    ////////////////////////


    S=n*m+1,T=n*m+2;
    ll op;cin>>op;
    for(int dx=1;dx<=op;++dx)
    {
        ll a,b;cin>>a>>b;
        mp[px][py]='X';//因为先手操作之后不能返回当前局面，所以要将这个位置置为X
        ll pre_1=gt();
        mp[px][py]='.';//
        swap(mp[px][py],mp[a][b]);
        px=a;py=b;

        mp[px][py]='O';//与上面改成X是同理的
        ll pre_2=gt();
        mp[px][py]='.';//
        // cout<<dx<<' '<<px<<' '<<py<<' '<<pre_1<<' '<<pre_2<<endl;
        if(pre_1&&pre_2)
        {
            ans.push_back(dx);
            //如果前后都是必胜态，那么该操作失误
        }
        ///
        cin>>a>>b;
        swap(mp[px][py],mp[a][b]);
        px=a;py=b;
    }

    cout<<ans.size()<<endl;
    for(auto i:ans) cout<<i<<endl;
}
int main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    solve();
    return 0;
}
博弈论
#学习笔记 #数学 #博弈论 #图论 #网络流
二分图博弈学习笔记
https://sophilex.github.io/posts/58faeac3/
作者
Sophilex
发布于
2023年12月19日
许可协议