SVD-LLM: TRUNCATION-AWARE SINGULAR VALUE DECOMPOSITION FOR LARGE LANGUAGE MODEL COMPRESSION

在近似矩阵参数\(W\)的背景下，即每一层的输入为\(X\)，那么目标可以表示为 \[ W^* = \mathop{\text{argmin}}\limits_{W'} ||W'X - WX||_{F}^2\tag{1} \] ASVD[[#^a3b6a4|[1]]]的做法是引入与输入\(X\)相关的可逆矩阵\(S\)，将\(WX\)改写为\((WS)(S^{-1}X)\)，并用SVD对\(WS\)进行近似。其将\(S\)取为 \[ S_{ii} = \left( \frac{1}{n} \sum_{j=1}^{n}|X_{ij}| \right)^{\alpha} \tag{2} \] 本文指出目前设计的\(S\)依然存在问题，贪心地对\(WS\)的最小奇异值方向进行去除并不能保证\(Loss = ||W'X - WX||_{F}^2\)最小。本文将\(S\)设计为\(XX^T\)的Cholesky decomposition，即满足 \[ SS^T = XX^T \tag{3} \] 且\(S\)是一个下三角矩阵，这里记为\(S_{Cho}\) 在这种设计下，再对\(WS_{Cho}\)进行SVD分解，可以做到\(Loss\) 与删除的奇异值\(\sigma_{i}\)是一一对应的，从而可以从理论上保证贪心策略的有效性。

具体来说，其证明了，当\(S_{Cho}\) 是\(XX^T\)的Cholesky decomposition，且对\(WS_{Cho}\)进行SVD分解并去除第\(i\)个奇异值对应向量时，有 \[ Loss = ||W'X - WX||_{F}^2 = \sigma_{i}^2\tag{4} \] 并且，如果同时去除\(\sigma_{m+1},\sigma_{m+2},\dots , \sigma_{r}\)的话，可以得到 \[ Loss = ||W'X - WX||_{F}^2 = \sum_{j=m+1}^{r}\sigma_{i}^2\tag{5} \] 具体证明过程略过。这还是非常神奇且强大的。

另外其还指出在略去一些参数之后，还应该重新对参数进行微调。记近似之后的结果为 \[ WS_{Cho} \approx U_{k} \Sigma_{k} V_{k}^T\tag{6} \] 记 \[ W_{u}' = U_{k} \Sigma_{k}^{1/2}, W_{v}' = \Sigma_{k}^{1/2}V_{k}^TS_{Cho}^{-1} \] 这里把多出来的\(S_{Cho}^{-1}\)放进来，那么此时\(W_{u}'W_{v}'\)就是最终的近似参数了。我们应当对\(W_{u}'\)和\(W_{V}'\)都进行LoRA微调。 \[ W_{u}' \leftarrow W_{u}' + B_{u}A_{u}, \ \ W_{v}' \leftarrow W_{v}' + B_{v}A_{v} \] 但是由于它们来自于\(WS_{Cho}\)的分解，是相互关联的，两者分开单独微调的话，会有一定影响。 因此作者提出分别微调 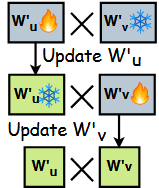先冻结\(W_{v}'\)，微调\(W_{u}'\)；再冻结\(W_{u}'\)，更新\(W_{V}'\)

从结果上来看，效果还是很惊艳的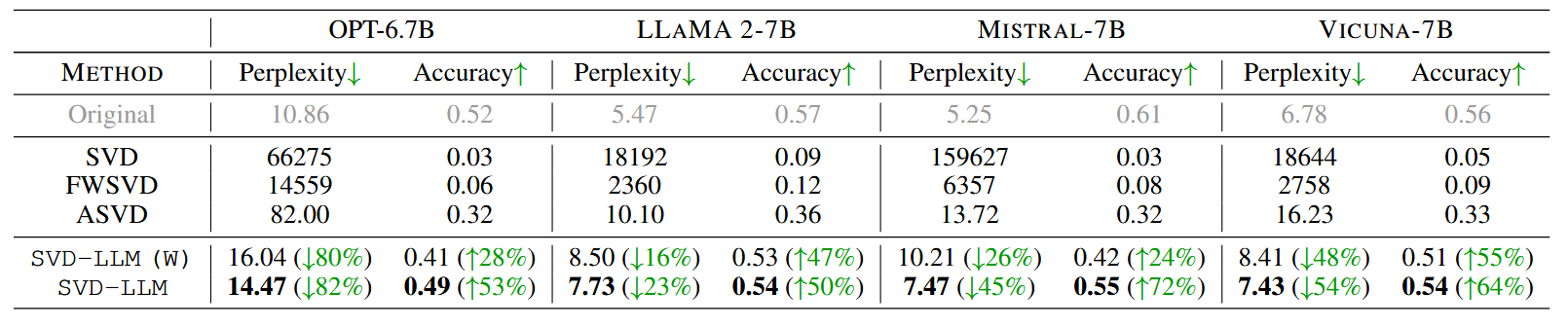

SVD-LLM(W)代表只使用\(S_{Cho}\)，不进行分解近似后的微调。

Reference

[1] Yuan, Z., Shang, Y., Song, Y., Wu, Q., Yan, Y., & Sun, G. (2023). ASVD: Activation-aware Singular Value Decomposition for Compressing Large Language Models. ^a3b6a4