TD3: Tucker Decomposition Based Dataset Distillation Method for Sequential Recommendation

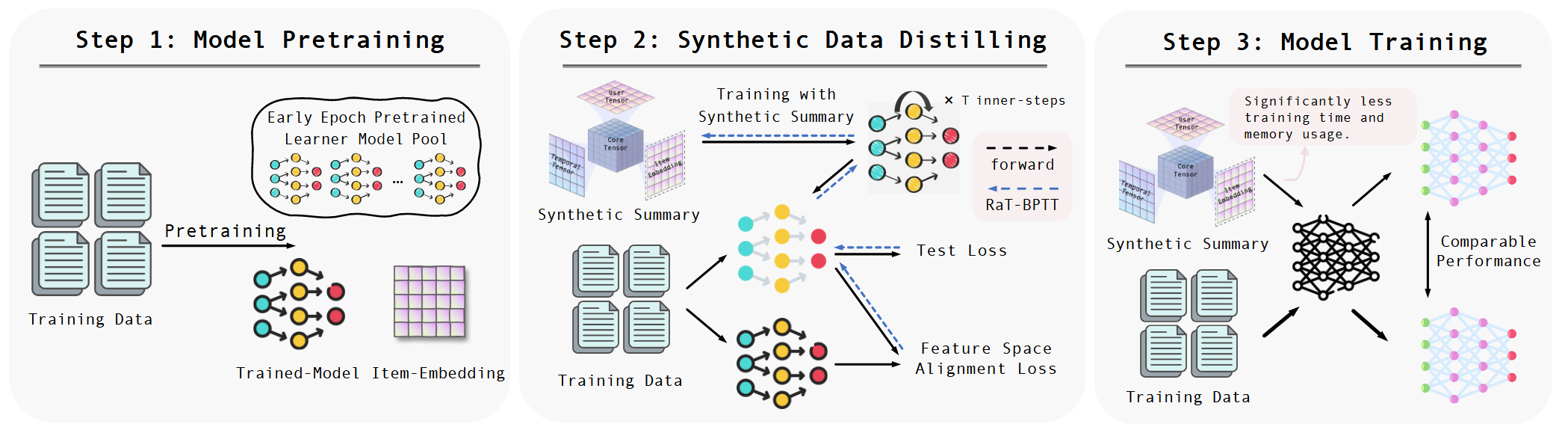
主要针对序列推荐数据集的蒸馏。传统的推荐数据集蒸馏方法通常生成独立的合成交互，这些交互无法捕捉序列数据固有的时间依赖性，简单地将独立生成的交互组织成序列并不能保证保留时间上的依赖信息。 此外，推荐数据集蒸馏自然面对着数据离散性对优化的挑战。普遍的解决手段是item参数化，优化得到其分数，然后依分数采样得到最终数据集。但是这也导致一个问题：参数量与数据集大小强相关，对计算，优化的压力都很大。

首先，原始数据集表示为\(\tau = \{x_{i}\}_{i=1}^{|\tau|}, \ x_{i} = [x_{ij}\in V]_{j=1}^{|x_{i}|}\)，用户，样本集合为\(U,V\)。要合成的序列推荐数据集，可以参数化表示为\(S\in R^{\mu \times \zeta \times |V|}\)，分别代表user，时间t，以及每一个item的概率。

内部推荐模型做优化的时候，对于每一个交互，作者并没有选择一个固定的item的embedding作为输入，而是将\(S\)的最后一维与提前训好的embedding矩阵相乘，相当于对候选items的embedding做了加权。这当然也是有道理的，本身\(S\)也是学习得到的，不过这一点与之前工作还是不太一样的。事实上这种操作也带来了一个好处：最后不需要对item依据分数采样，也就省去了诸如DconRec中引入gumbal softmax之类的麻烦。

说回面临的挑战，其中之一是参数量与数据集强相关。直接将参数规模做到与数据集规模解耦在推荐场景下可能不是特别现实？不过对参数矩阵引入分解还是可以极大缓解参数压力。作者引入Tucker分解，将\(S\in R^{\mu \times \zeta \times |V|}\)分解为\(S = G \times_{1} U \times_{2} T\times_{3} E\)。其中\(G\in \mathbb{R}^{d_{1},d_{2},d_{3}}\)用于建模其余因子之间的关系，\(U\in \mathbb{R}^{\mu \times d_{1}}\)表示合成用户的相关信息，\(E\in \mathbb{R}^{\zeta \times d_{2}}\)表示时间信息，\(P\in \mathbb{R}^{|V|\times d_{3}}\)代表item信息。 Tucker分解固定将张量分解为四个小张量，这里作者直接赋予了它们与推荐场景相关的含义，也算有道理吧。其中\(E\)可以直接用embedding信息替换，不需要训练，其它矩阵梯度下降优化。

至于两层优化的对应手段，比较常规，内层用KLD对齐要预测item的概率。当然考虑到前面提到的序列依赖性，这里不能只对齐最后一个item，前面的item也要对齐。外层就是推荐模型的feature对齐。

亮点还是提出参数量随数据集规模增长这个问题以及Tucker分解的引入，分解得到的三个因子刚刚好对应了矩阵\(S\)的三个维度hhh。这块可能也还有发展空间。