RETAINING BY DOING: THE ROLE OF ON-POLICY DATA IN MITIGATING FORGETTING
通常认为，SFT使用的FKL(mean-seeking)，相比于RL对应的RKL(mode-seeking)，更能保留分布信息，从而在llm灾难性遗忘问题上有较好的缓解，但是本文提出，在原本的分布多模态假设下，RL可以在尽可能保留原本旧模态分布的情况下，学习新的模态，从而相比于SFT，在遗忘问题问题上有更好的表现。
同时，作者指出，这一行为主要来自RL的on-policy训练数据，而非其相对SFT多出来的KL正则化项或者优势函数估计。
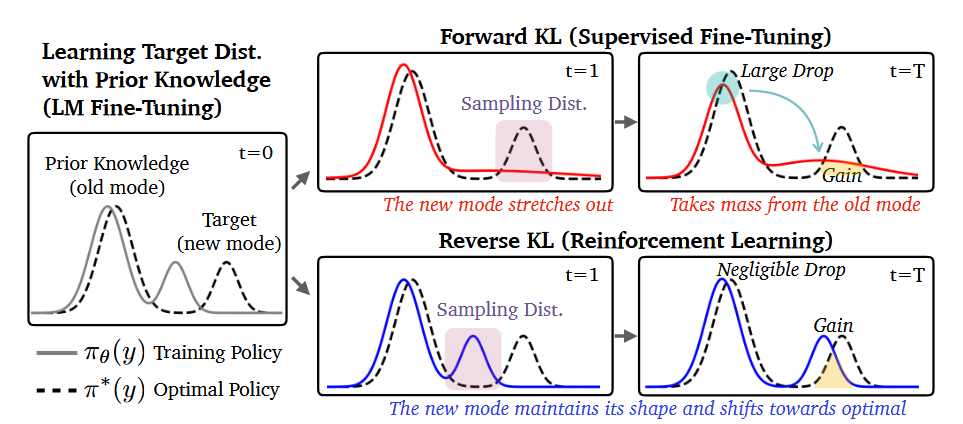
Revisiting RKL and SKL
对于第一个结论，作者将最优策略分布\(\pi^*\)建模为两个Gaussion分布的混合： \[ \pi^*(y) = \alpha^* p_{old}(y;\theta_{old}^*) + (1-\alpha^*) p_{new}(y;\theta_{new}^*)\tag{1} \] 其中\(p_{old}\)代表旧知识，\(p_{new}\)代表新知识
当我们将初始策略固定为单模态时：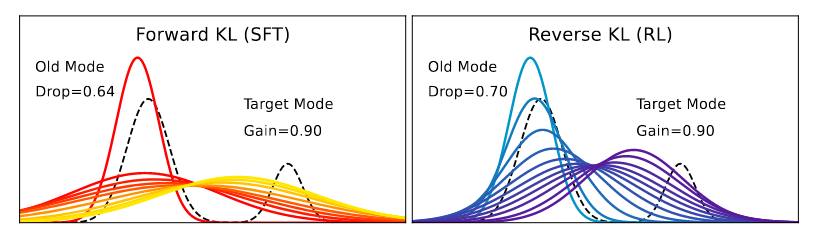 
图中红色->黄色，蓝色->紫色代表训练过程的不断推进。可以看到，
FKL尝试覆盖全部模态，对于旧知识会有相当一部分保留，而RKL在mode-seeking行为下会更加激进，从而导致原有知识的大量丢失，这一点可以通过Drop值来体现。
但是在LLM场景下，策略分布往往更可能本身就是多峰的： \[
\pi_{\theta}(y) = \alpha q_{old}(y;\theta_{old}) +
q_{new}(y;\theta_{new})\tag{2}
\] 其中\(q_{old}\)在预训练或者其它任务的微调之后，已经可以较好地覆盖目标分布\(p_{old}\)，目标是让\(q_{new}\)去逼近\(p_{new}\)，同时尽可能保持\(q_{old}\)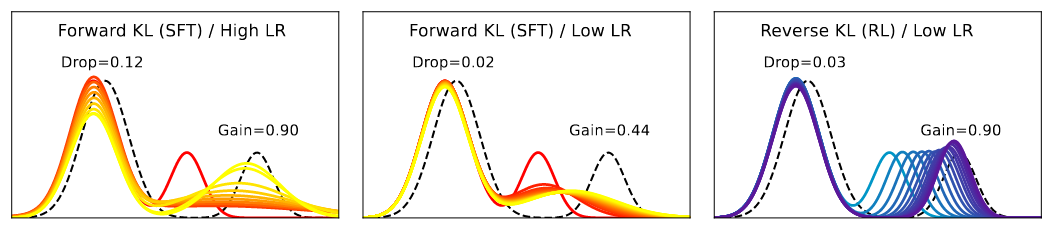 
- FKL: 同样尝试让整体分布去匹配目标，但是这会牺牲旧模式的匹配度，在高学习率下，为了更快匹配，对\(q_{old}\)的改变会更大，甚至改变混合系数\(\alpha\)
- RKL: \(q_{new}\)很好地拟合了\(p_{new}\)，但是同时\(q_{old}\)也基本没有损失。注意到\[ RKL(p(X),q_{\theta}(X))= E_{x\sim q_{\theta}(X)}\left[ \log \frac{q_{\theta}(x)}{p(x)} \right]\tag{3} \]RKL关注的是q中有概率的地方，p也必须有，从而可以避免在波谷处过度拟合。而原本的\(q_{old}\)已经拟合的不错了，这部分并不会产生多少Loss，从而其可以专心拟合\(p_{new}\)
总之，在对初始分布给出不同的假设之后，可以得到与之前工作截然相反的结论：
RL相比SFT，在新任务上训练之后，可以有更好的防止遗忘旧任务的能力
这个toy实验本身也并非足够完善，分布混合的模式，权重不同，也许会有其它结论，不过其本身给出了反例，可以说明之前的结论并不一定是正确的，尤其是在LLM场景下。
On-policy data training
作者之后探讨了一下RL这种mode-seeking的行为，实际上是来自于on-policy的数据使用。目前RL与SFT的主要区别有：
- RL一般使用on-policy数据，SFT一般使用off-policy数据
- RL的目标函数一般是\[ L_{RL}(\theta;x) = E_{y\sim \pi_{\theta}(\cdot|x)}[r(x,y)] - \beta D_{KL}(\pi_{\theta}(\cdot|x)||\pi'(\cdot|x))\tag{4} \]其相比于SFT，多出来一个KL正则化项
- RL对advantage的运用，导致其对数据梯度进行了一个加权，而在SFT，所有样本梯度的权重是一致的，这一点在REINFORCE with baseline的梯度表达式上可以非常直观的看到:\[ \nabla loss(x) = E_{(a_{t}, s_{t})\sim \pi}[\nabla \log\pi(a_{t}|s_{t}) \ A(t)]\tag{5} \]
在做了一系列对比实验之后，作者指出，on-policy的数据运用，是导致上述mode-seeking行为的主要原因。
Applying on-policy strategy to SFT
利用这一点，我们显然也可以尝试对SFT进行on-policy的数据运用来尝试缓解灾难性遗忘。这个的成本是高昂的，但是如果做一个权衡：
每隔一段训练时间，用当前模型重新生成数据并进行筛选，在这些新生成的数据上再做SFT
这类似于on-policy，虽然更新频率相比于RL会更低，但是仍然可以享受到缓解灾难性遗忘的好处。
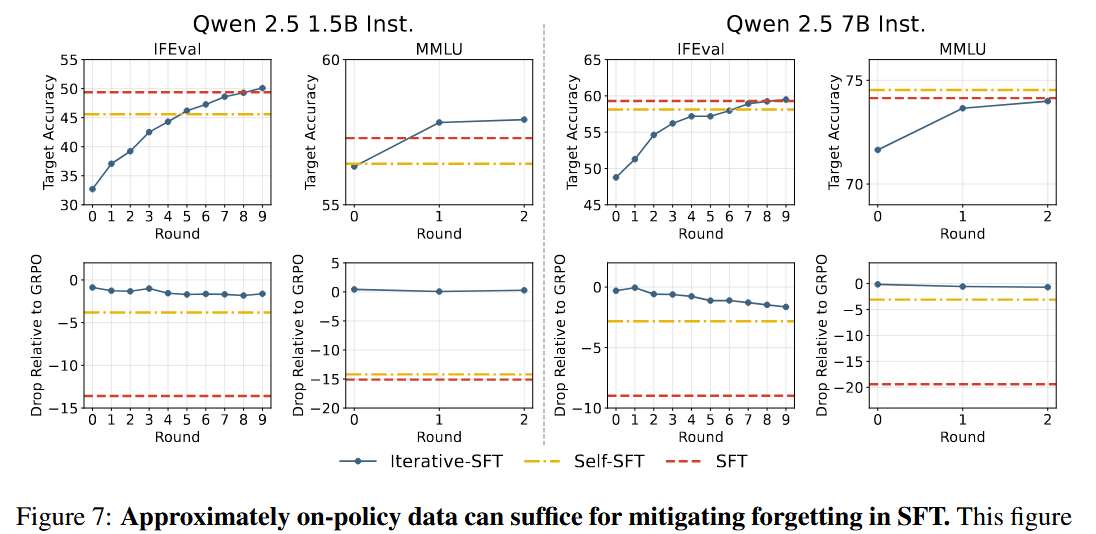
Conclusion
本文指出mode-seeking行为相比于mean-seeking，在LLM场景的分布多模态假设下，在学习新分布的时候，可以更好的保留原分布，从而缓解灾难性遗忘问题。 并且指出这一行为主要来自于on-policy的数据运用。