ASVD: ACTIVATION-AWARE SINGULAR VALUE DECOMPOSITION FOR COMPRESSING LARGE LANGUAGE MODELS

ASVD提出使用SVD分解来做到用较少参数近似LLM参数，从而减小模型规模，算一种post-training。这一思想个人感觉与KD算是正交的。前者减小现有模型规模，而后者是在两个模型上转移知识，且学生模型的架构是提前设置好的。 首先目标是比较明晰的，我们考虑每一层的线性层参数\(W\)，以及其输入\(X\)，参数的最优近似结果\(W_{k}^*\)应当满足 \[ W_{k}^* = \mathop{\text{argmin}}\limits_{W_{k}} ||W_{k}X - WX||_{F}^2\tag{1} \] 其中\(k\)代表秩为\(k\)的近似。 这里我们考虑了每一层的输入\(X\)，从而\((1)\)式实际上是在对齐两种参数下的输出空间，而不仅仅是对齐参数。这是因为对模型已有参数进行近似，应当是task-targeted，而这一点在简单对齐参数的情况下可能是难以满足的。事实上[2]对此现象也有所描述,这里不再赘述。

那么在\((1)\)式下，我们直接对参数\(W\)做SVD分解，然后保留前\(k\)大的奇异值方向，极有可能是不够优的。作者提出引入一个来自参数\(X\)的可逆矩阵\(S\)，并且将\(WX\)改写为 \[ W = (WS)(S^{-1}X)\tag{2} \] 那么让\(W_{k}\)近似\(WS\)即可，后半部分只跟输入\(X\)有关。那么我们按照SVD的套路对WS进行分解，并保留前k大奇异值方向进行近似。具体来说 \[ WS=U'\Sigma' V'^T \tag{3} \] 保留前\(k\)大奇异值后得到 \[ WS \approx U_{k}'\Sigma_{k}' V_{k}'^T = W_{k} \tag{4} \] 事实上也不难看出引入\(S\)的目的: 在分解，近似的过程中加入对当前层输入\(X\)的考虑，直观上对靠近\((1)\)式最优解\(W_{K}^*\)是有帮助的。

但是如何引入\(X\)也是有讲究的。ASVD中将\(S\)设置为一个对角阵 \[ S_{ii} = \left( \frac{1}{n} \sum_{j=1}^{n}|X_{ij}| \right)^{\alpha} \tag{5} \] 其没有解释这一设计的具体理由，可能也是试出来的吧

另外其对模型中不同层对压缩的敏感性也做了探究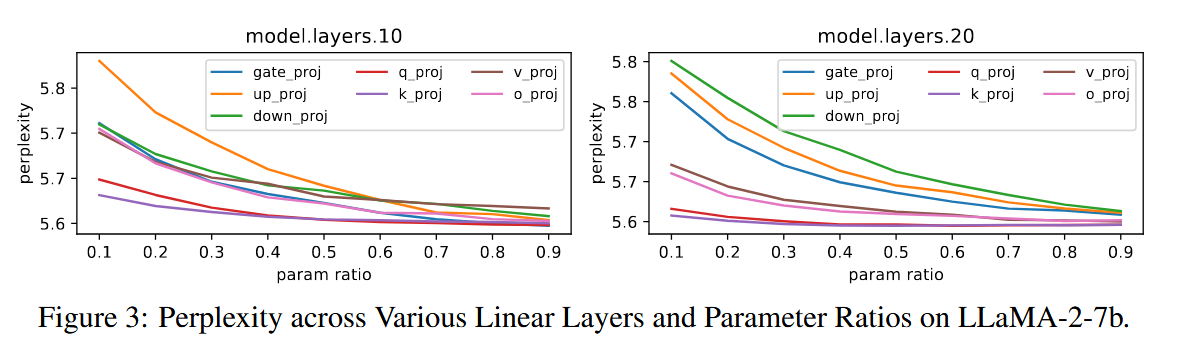

如图，横轴代表不同的压缩比，纵轴代表perplexity用来表示性能。可以看到不同层之间对压缩的敏感性不同，但是都表现出了压缩比越高，性能越差的结果(显然)。

由此我们应当对不同层采用不同的压缩比，这一点在文中是通过二分实现的，这里不再赘述。

Reference

[1] Yuan, Z., Shang, Y., Song, Y., Wu, Q., Yan, Y., & Sun, G. (2023). ASVD: Activation-aware Singular Value Decomposition for Compressing Large Language Models.  ^132f6c

[2] Hsu, Y., Hua, T., Chang, S., Lou, Q., Shen, Y., & Jin, H. (2022). Language model compression with weighted low-rank factorization. In ICLR, 22 ^942a0c